2 三角関数:2.加法定理 21 加法定理;オイラーの式を利用すると、指数関数の諸定理を利用して 三角関数の公式を導出することができる。 三角関数の公式に比べて、指数関数の公式、はるかに単純であるから 公式の証明の容易である。以上が三角関数の微積分のスライド性です。 3 三角関数の積分まとめ 以上が三角関数の積分の公式と性質です。 特に、現実世界の問題に微分積分学を応用するには、お伝えした3つの性質を知っておくことがとても有用です。
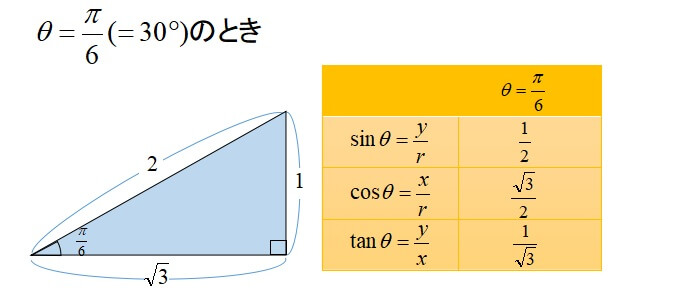
三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com
数 2 三角関数 公式
数 2 三角関数 公式-加法定理の2つの式を辺々加えることで、 積和の公式 が得られます。 積和の公式とは、2つの三角関数の積を、三角関数の和(・差)の形に変換する公式です。 sinαcosβ = 1 2{sin(α β)sin(α −β)} cosαsinβ = 1 2{sin(α β)−sin(α −β)} cosαcosβ = 1 2{cos(α β) cos(α− β)} sinαsinβ = − 1 2{cos(α β)− cos(α −β)} sin α cos 三角比は図形的な意味に注目 し、 三角関数は数に注目 しています。 図形的性質を考える場合は180°を超えることはないです。 2つの線分のなす角は最大で180°ですからね。



数2 三角関数 性質
三角関数の相互関係: sin 2 θ cos 2 θ = 1 \sin^2\theta\cos^2\theta=1 sin2θ cos2 θ = 1 tan θ = sin θ cos θ \tan\theta=\dfrac {\sin\theta} {\cos\theta} tanθ = cosθsinθ 1 tan 2 θ = 1 cos 2 θ 1\tan^2\theta=\dfrac {1} {\cos^2\theta} 1 tan2θ = cos2θ1 三角関数の相互関係の公式 6 三角関数の式の値 7 三角関数の等式の証明 8 三角関数の性質① 9 三角関数の性質② 10 三角関数のグラフ① 11 三角関数のグラフ②(縦幅の変化) 12 三角関数のグラフ③(周期の変化) 13 三角関数のグラフ④(平行移動) 1423 積 ⇄ 和の公式、合成;
いろいろな公式があって、何がしたいのかわからない問題って多いですよね。でも、三角関数の問題って 突き詰めていくと意外にシンプル で、 重要なテーマが2つに絞れる んです。 三角関数でよく狙われるテーマは、 「三角関数を用いた方程式・不等式」と「三角関数の最大・最小」 で →三角関数の3通りの定義とメリットデメリット ・三角関数の相互関係 →三角関数の相互関係とその証明 ・三角関数の性質 →90°θ,180°θなどの三角比の公式と覚え方 ・三角関数のグラフ ・偶関数,奇関数 →偶関数と奇関数の意味,性質などまとめ ・三角関数を含む方程式,不等式高校数学2で学習する「三角関数」ではさまざまな公式が出てきます。 三角比や半角や2倍角、加法定理、合成など・・・ でも加法定理さえ覚えておけばほとんどの公式を導出できます。 三角関数の合成
ラジオ第2放送毎週 水曜日・木曜日 午後7:50〜8:10 ※この番組は、21年度の新作です。 整式・分数式の計算 3次の乗法公式と因数分解(1) 3 4/14 3ピタゴラスの定理 や オイラーの公式 などから以下の基本的な関係が導ける 。 cos 2 θ sin 2 θ = 1 {\displaystyle \cos ^ {2}\theta \sin ^ {2}\theta =1\!} ここで sin2 θ は (sin (θ))2 を意味する。 この式を変形して、以下の式が導かれる: sin θ = ± 1 − cos 2 θ {\displaystyle \sin \theta =\pm {\sqrt {1\cos ^ {2}\theta }}}三角関数を扱う場合には,積分に限らず次数に注目する必要があります。なぜなら,2倍角の公式や3倍角の公式 \\begin{array}t{l} \sin 2x = 2 \sin x \cos x \\ \cos 2x \begin{array}t{l} = \cos^2 x \sin^2 x \\ = 2\cos^2 x 1 \\ = 1 2\sin^2 x \end{array} \\ \displaystyle \tan 2x = \frac{2 \tan x}{1 \tan^2 x} \\8px \cos 3x = 4 \cos^3 x 3 \cos




ม 5 โน ตของ 数2 三角関数のグラフ ช น Senior Clear




三角関数04 還元公式 Youtube
次に紹介するコタンジェントやセカントなどは、高校数学や大学受験では用いないのが通常だが、つぎのコタンジェントなどの関数も三角関数である。 cot θ = x y {\displaystyle \cot \theta = {\frac {x} {y}}} sec θ = 1 x {\displaystyle \sec \theta = {\frac {1} {x}}} csc θ = 1 三角関数の2倍角の公式・半角の公式の証明と応用 スポンサーリンク 高校数学Ⅱ 三角関数 検索用コード 証明は容易で,\ \bm {加法定理において\ \beta\ →\ \alpha\ }とするだけである \bm {利用機会が極めて多い}ので,\ 毎回加法定理から導くというのは "2倍角の公式"の証明 半角の公式 半角の公式 \(・sin^2\frac{α}{2}=\frac{1-cosα}{2}\) \(・cos^2\frac{α}{2}=\frac{1cosα}{2}\) "半角の公式"の証明 三角関数の合成 三角関数の合成 $$asinθbcosθ=\sqrt{a^2b^2}sin(θα)$$ "三角関数の合成"の証明 積和の公式 積和の公式



数2 三角関数 性質
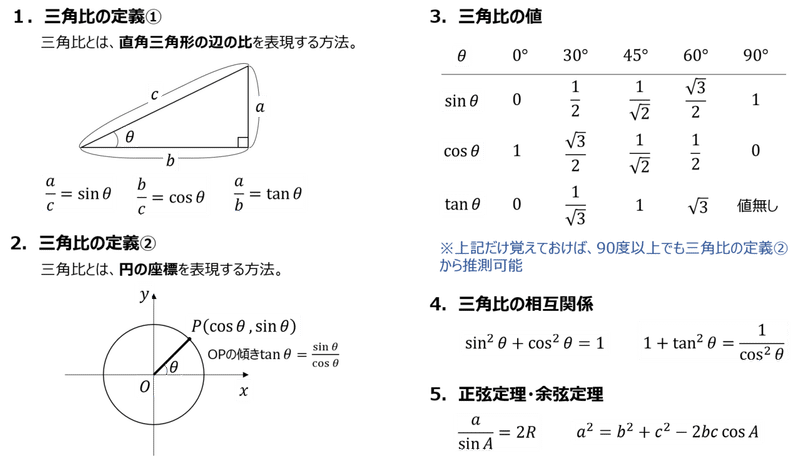



三角比は1時間で解けるようになる 箕輪 旭 Note
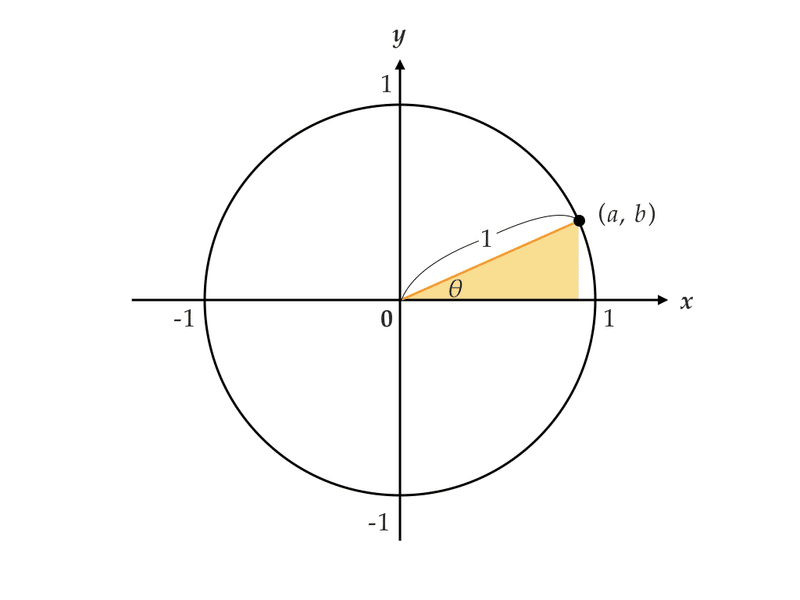
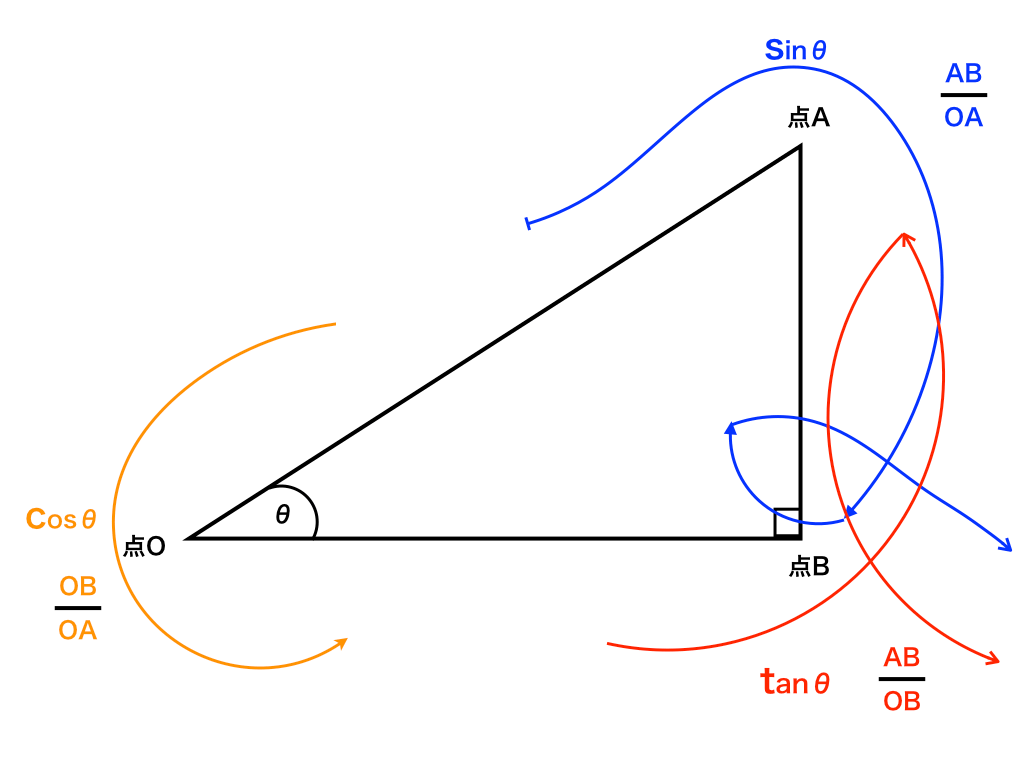
ここからは、高2数学に出てくる主な公式の動画解説を紹介します。どの動画も、公式を分かりやすく解説している人気の動画となっています。ぜひ、参考にしてください。 数学Ⅱ まずは、数学Ⅱに出てくる主な公式の解説動画から紹介します。 三角関数とその基本的な性質三角関数の公式の確認 とする ,余弦 の2倍角 公式より 半角の公式 2 2 Microsoft Word 数2_加法倍角定理doc Author SoYoshida Created Date 7/8/10 AM原点 を中心とする半径 の円周上にある点 の座標を とする.(ただし,半径 はつねに正,座標 は正,負,0の値をとる符号が付いている) 動径 が 軸の正の向きをなす角度を とするとき,次の比の値は(相似図形の性質から)半径 の大きさに関係なく,角度 だけで定まる.そこで, の関数
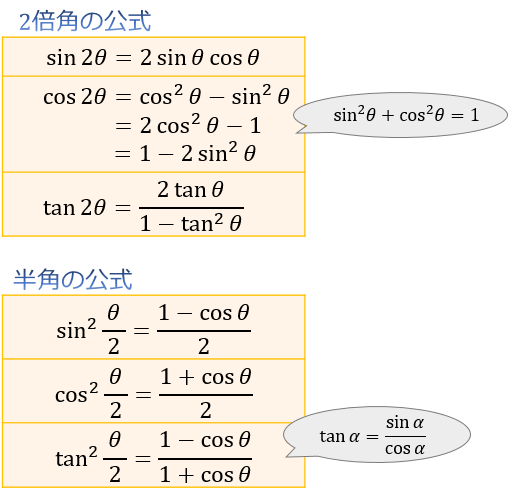



2倍角の公式 半角の公式とその証明 二等辺三角形で分かる2倍角の考え方 アタリマエ




三角関数は2時間で解けるようになる 外資系コンサルタントが主夫になったら
による有理関数表示(※数IIIの三角関数の積分等で使用) sin = 2sin 2 cos 2 cos = 2cos2 2 1 tan = 2tan 2 1 tan2 2 = 2 sin 2 cos 2 cos2 2 = 2 1 1tan2 2 1tan2 2 1tan2 2 = 2t 1 t2 = 2tan 2 1 1tan2 2 = 1 tan2 2 1tan2 2 = 2 t 1t2 = 1 2 1t2 三角関数公式三角関数の性質と相互関係 三平方の定理による三角関数の計算(1) / 三平方の定理による三角関数の計算(2) / θ と θ+ π 、θ- π の関係 / θ と θ+ ( π /2)の関係 / sinθ+cosθとsinθcosθの関係 / sinθ+cosθ、sinθcosθとsin^3θ十cos^3θ / sinθ-cosθとsinθcosθの関係 / sinθ-cosθ、sinθcosθとsin^3θ-cos^3θ / 三角関数の相互関係を用いる証明 高2 数2 (三角関数の性質)公式まとめ 高校生 数学のノート Clear 表紙 1 2 公開日時 年10月19日 22時35分 更新日時 21年04月24日 13時16分 高校生 2年生 数学




高校数学 半角の公式とは 映像授業のtry It トライイット




高校数学 三角関数の相互関係と還元公式 負角の公式 補角の公式 余角の公式 受験の月
26.複素数における指数関数と三角関数 実数の範囲では三角関数と指数関数は全く別種の関数でしたが、複素数の範囲に拡大するとオイラーの公式 e iθ =cosθ+i・sinθ (242) より、三角関数が指数関数に統合されこれらの関数は同種の関数として扱うこと公式集:三角関数 加法定理 合成公式 三角関数計算の基礎 2倍角の公式 3倍角の公式 積和の公式 和積の公式== 三角関数の値 ==(90゜~180゜) 解説 印刷物になっている三角関数表は 0 °~ 90 °の値のみ書かれており, sin 118 °のような値は書かれていない. 右図から次の公式が導かれ,これを利用すれば, 90 °~ 180 °の三角関数の値を, 0 °~ 90 °の三角関数に直して求めることができる.
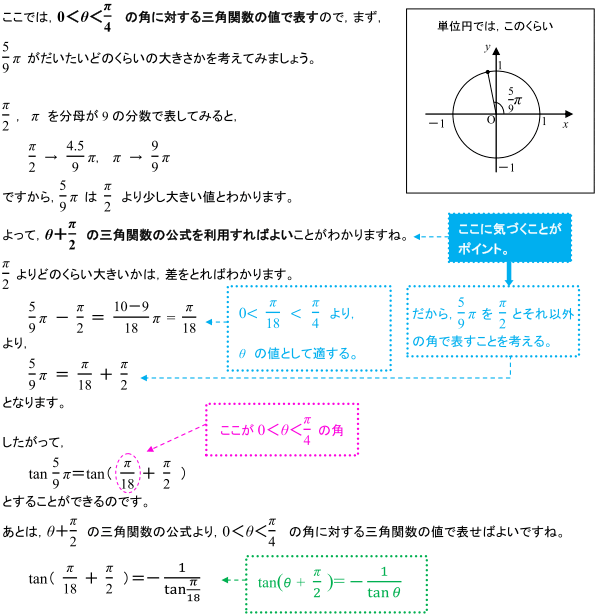



0 8 P 4 の角に対する三角関数での表し方 数学 苦手解決q A 進研ゼミ高校講座



三角関数公式一覧表
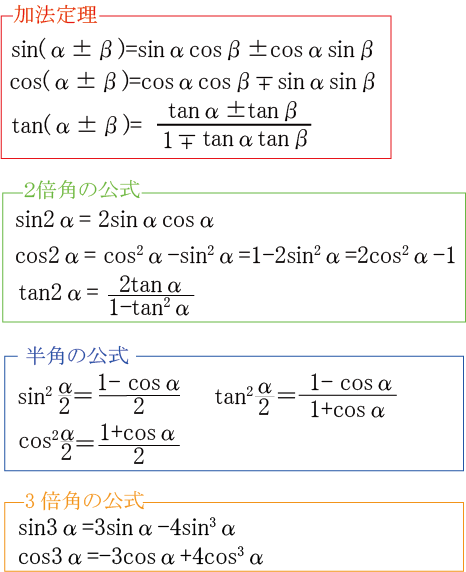
このページでは,はじめに, sin ( α β) , cos ( α β) などの ( )をはずす公式 「三角関数の加法定理」 を解説し,その応用として 「2倍角公式」「3倍角公式」「積和の公式」「和積の公式」 を解説する. (1) (2)の証明・・・ (以下の証明は第1象限の場合についてのものであるが,この公式は, α , β が任意の角の場合でも成立する.) 右図において, ∠ AOB= α22 指数関数の公式 指数法則axy = axay (ax)y = axy a0 = 1 d dx ex = ex d dx ax = (lna)ax 級数展開と近似公式 1 ex = ∑1 n=0 xn n!2 4 (三角関数の和から積の公式)となる。 eは無理数で,その値はe= であることが知られている。(裏面参照)




数学 三角関数の公式まとめ 加法定理 変換 合成 理系ラボ




三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要
学年 高校2年生, 単元 三角関数, キーワード 三角関数,2倍角,2分の1角,半角,sinθcosθtanθ,三角比,3角関数,3角関数=2sinαcosαcosα(12sin 2 α)sinα=2sinα(1sin 2 α)(12sin 2 α)sinα = ・・(19) (3)(1)(15)より <cosαの3倍角公式> =cos(2αα) =cos2αcosαsin2αsinα=(2cos 2 α1)cosα2sinαcosαsinα =(2cos 2 α1)cosα2(1cos 2 α)cosα = ・・()2次関数 例題(9) 練習問題 練習問題+解答図形と計量 例題(12) 練習問題 練習問題+解答 正弦定理 余弦定理 三角形の面積(ヘロンの公式) 三角比の値 練習プリント 三角比の値 練習プリント+解答 al教材三角形を解く三角形の決定条件




三角関数 8倍角の公式 Canada S Windview




数学 三角関数の公式まとめ 加法定理 変換 合成 理系ラボ
2 x ≪ 1 の時、ex ˘ 1 x 23 指数関数と三角関数の関係 指数関数の級数展開の式に、x = i (i は虚数単位) を代入し、三角関数の級数展開と比 較する 三角比・三角関数の公式一覧。 正弦・余弦・加法定理など このページでは、 三角比・ 三角関数 の公式 をまとめています。 予習・復習に役立てていただければ嬉しいです。 2数 の相加平均を グラフの性質、もしくは、三角関数の加法定理を使えば間違えずに作れるようになります。 を被積分関数という。 公式というわけではなく、定義なので注意してく




三角関数の微分 公式の証明と例題 高校生向け受験応援メディア 受験のミカタ
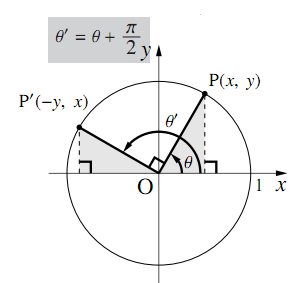



8 P 2の三角関数 数学ii フリー教材開発コミュニティ Ftext
高校数学の授業内容を想定して,自宅で学習できるよう工夫したプリントです。毎日の授業の予習や復習に,自宅で自分ペースで学習したいとき等に活用してください。数学Ⅰ01 数と式( 準備中です )学習プリント( 準備中です )学習プリント数学Ⅱの三角関数で使う公式 三角関数の性質 ※nは整数とする。 正弦の加法定理 ・sin(αβ)=sinαcosβcosαsinβの証明 ・sin(αβ)=sinαcosβcosαsinβの証明 余弦の加法定理 ・co 2直線のなす角 ↑答えが分かったら画像をクリック↑ 2倍角の公式 ↑答えが分かったら画像をクリック↑ 半角の公式 ↑答えが分かったら画像をクリック↑ 三角関数の合成 ↑答えが分かったら画像をクリック↑ 積を和に直す公式



三角関数の公式 図的理解



Q Tbn And9gcryolrm Dxfwat4p1nhc1gjbk0qzj6wrbkjapaspbruhs7arqz3 Usqp Cau
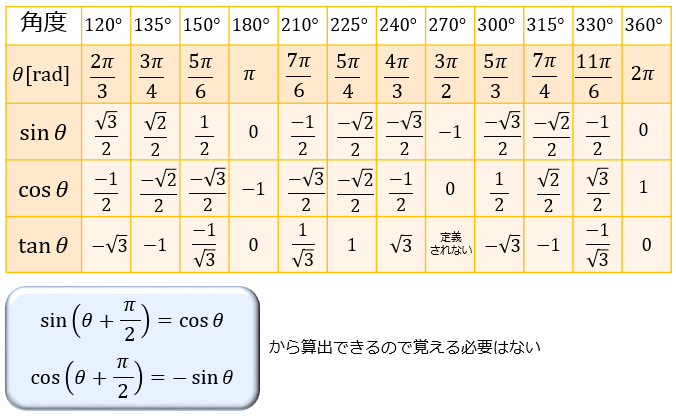



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ



3



三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com




三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com




三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com
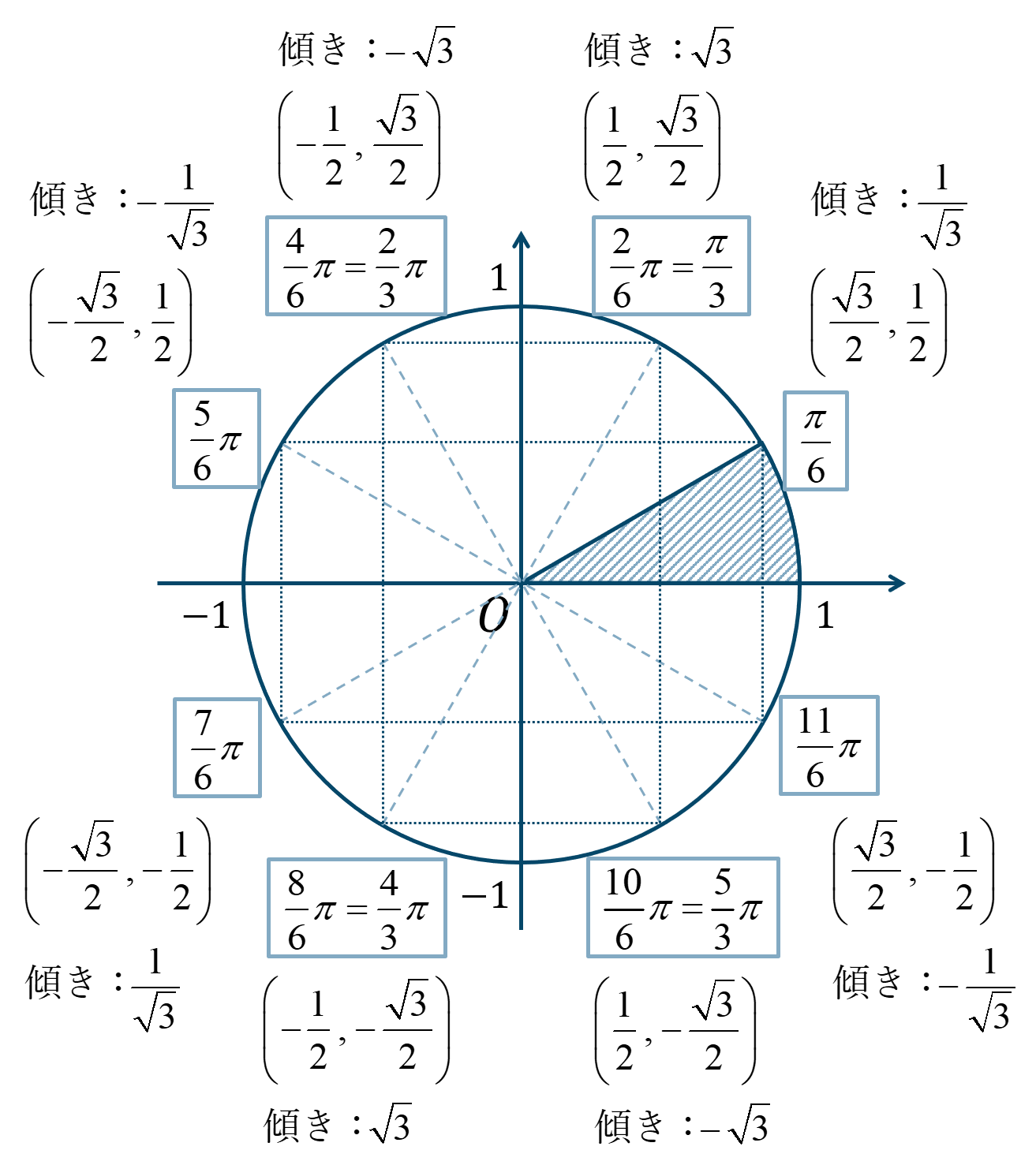



数学 問題演習 単位円を用いた三角関数の値 教科書より詳しい高校数学
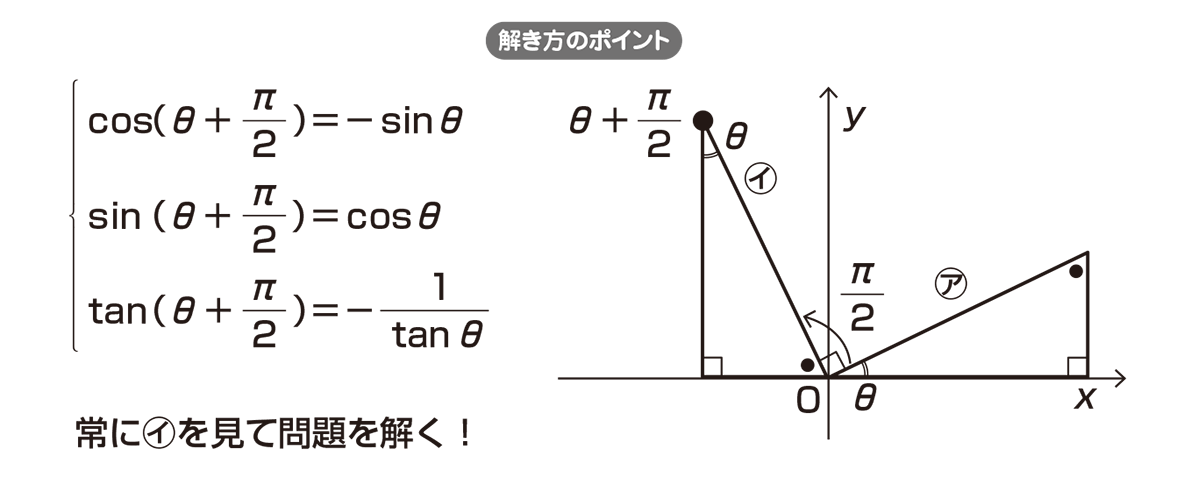



高校数学 8 と 8 P 2 の関係 映像授業のtry It トライイット



三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com




和積 積和 変換公式 おいしい数学




2倍角 3倍角の公式の導出 数学の偏差値を上げて合格を目指す
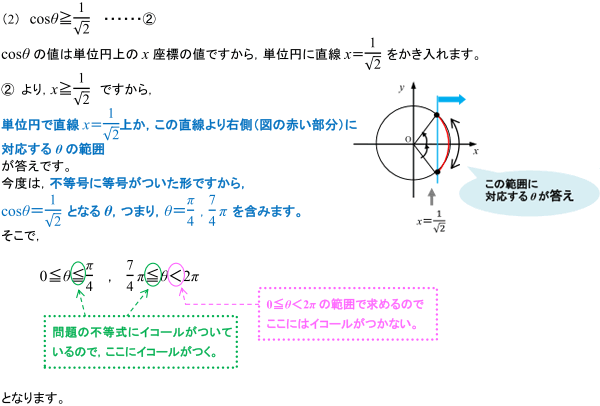



三角関数を含む不等式の解の求め方 数学 苦手解決q A 進研ゼミ高校講座




三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com




三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ




三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ




数学ii 2倍角 半角の公式 三角関数の合成の証明 Mike先生のstudyブログ




数学 三角関数 負角 余角 補角などの公式 Youtube



三角関数の証明付き公式集 重要公式をわかりやすく1から解説 Studyplus スタディプラス
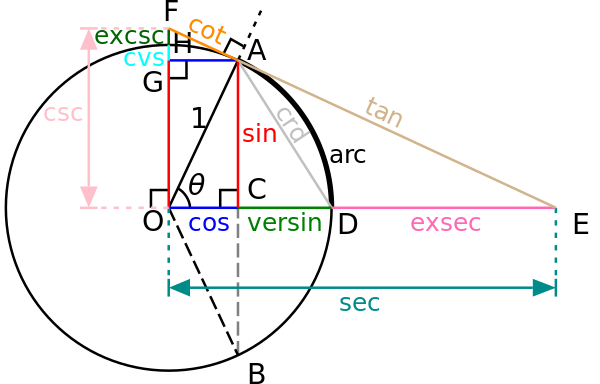



大学受験数学 三角関数 公式集 Wikibooks



第2章 三角関数




16 合成公式はsinだけじゃないんです 医学生gの数学ノート




三角関数とは 三角関数の基礎 試験にでる要点まとめ 高校生向け受験応援メディア 受験のミカタ




数 三角関数 半角の公式 オンライン無料塾 ターンナップ Youtube



三角関数の公式




数学 三角関数の公式まとめ 加法定理 変換 合成 理系ラボ




三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com




三角関数の性質 8 P 2の角の公式の証明 数学ii By ふぇるまー マナペディア




三角関数表 高校 数
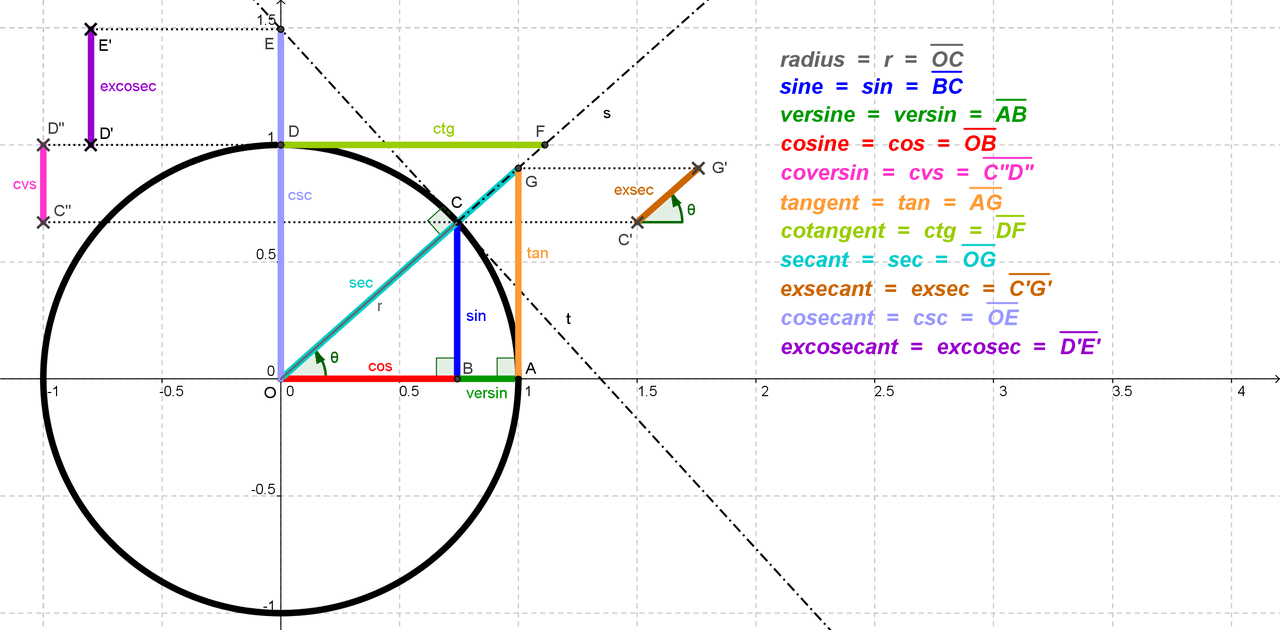



半角 二倍角の公式の覚え方は 覚えない事 その重要な意味と方法




高校数学 連立三角方程式 三角関数の相互関係 合成 加法定理の利用 受験の月




18個の公式にエピソードを吹き込む2016 怜悧玲瓏 高校数学を天空から俯瞰する




三角関数は2時間で解けるようになる 外資系コンサルタントが主夫になったら




高校数学 三角関数の合成 映像授業のtry It トライイット




数学 三角関数の公式まとめ 加法定理 変換 合成 理系ラボ




三角関数の性質 公式の覚え方 おときち副塾長 電脳空間学習塾かもん Youtube




三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ




三角関数 5倍角の公式 Canada S Windview




2倍角の公式と半角の公式 おいしい数学




三角関数 4倍角の公式 Canada S Windview



三角関数のグラフの書き方を徹底解説 周期や平行移動の問題も 受験辞典




原田 浩明 Sサクシード139 2倍角 半角 3倍角の値 公式は暗記より作れるように 高校 数学 数2 三角関数 2倍角 半角 3倍角 T Co K3devukzgj Twitter



三角比 三角関数の公式を単位円と関連づけて理解する 関谷 翔 Note
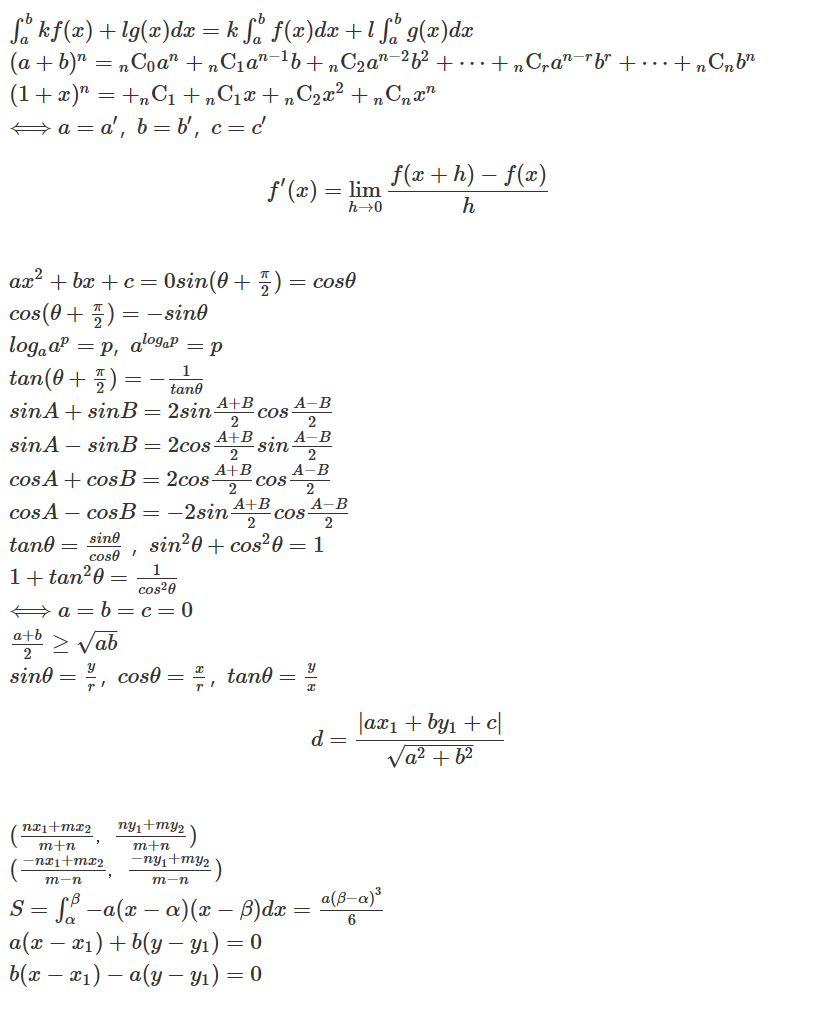



数学2編 完全攻略 高校数学の公式全部まとめてみたwww Cupuasu クプアス



三角関数の公式




高校数学 三角関数の最大 最小 2次同次式 受験の月




三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ
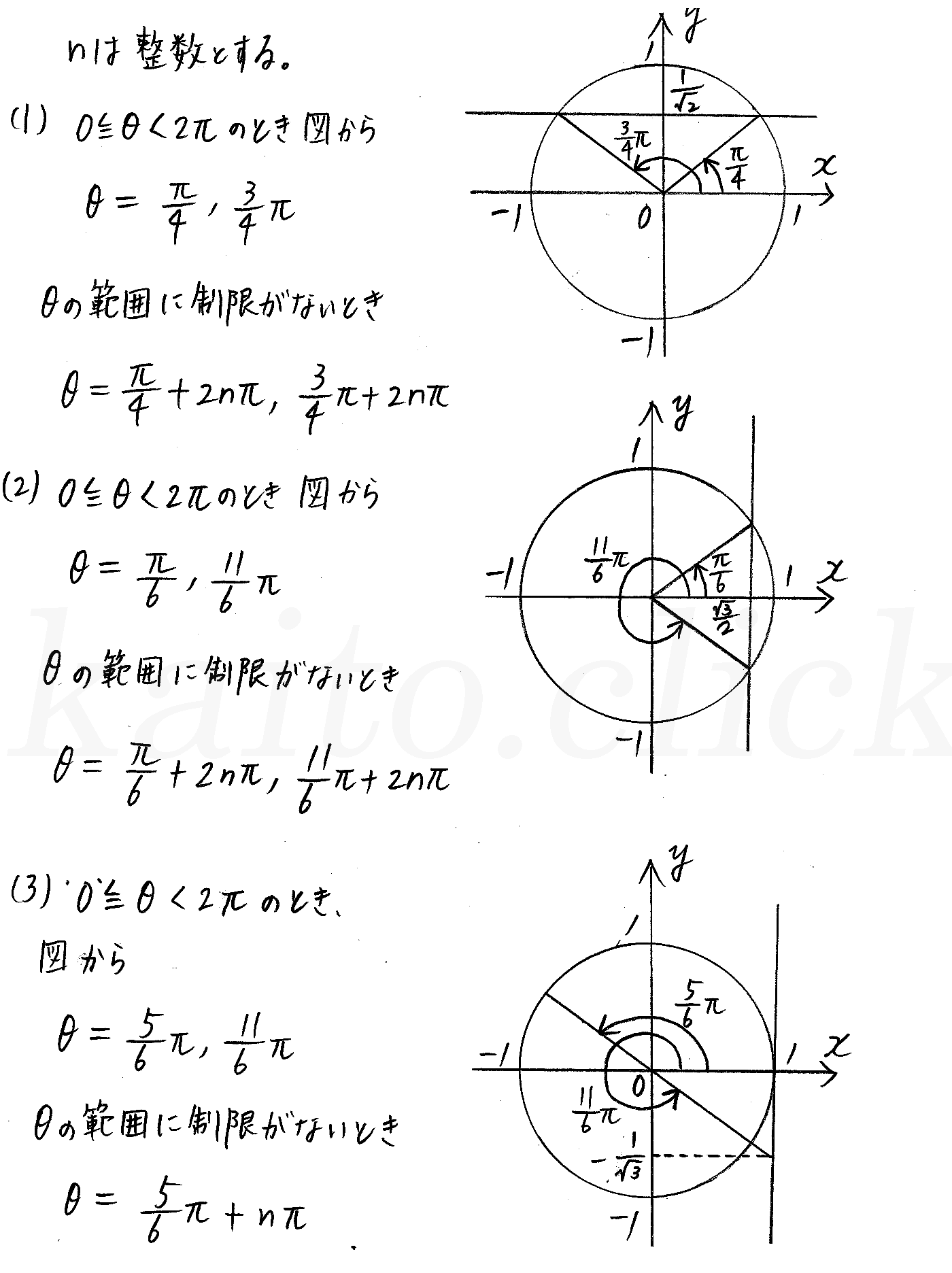



クリアー数学 数2 P58 25 三角関数を含む方程式 不等式




三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com



48s96ub7b0z5f Net Sankakukansuu Koushiki




三角関数講座その2 合成と方程式 最大値 高校数学の知識庫




三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要
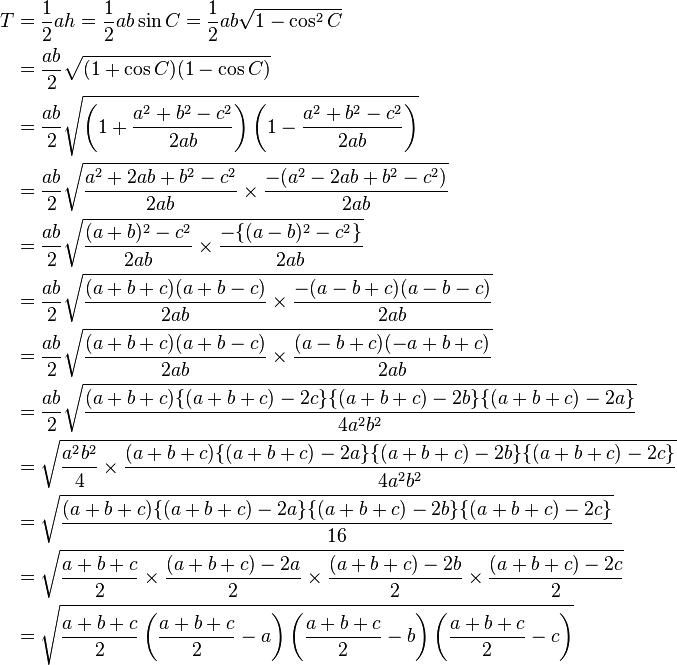



ヘロンの公式の証明 三角関数を使わずに ようこそ なるのホームページへ




三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com



三角関数の加法定理 倍角公式 3倍角公式 半角公式




三角関数の合成公式 証明 問題 Cos型について 理系ラボ




三角関数の還元公式 電気の神髄



三角関数の公式 Sin Cos Tan と覚え方




8 2np 8 8 P 8 P 2 P 8 P 2 8の三角関数 数学ii 三角関数 7 Youtube
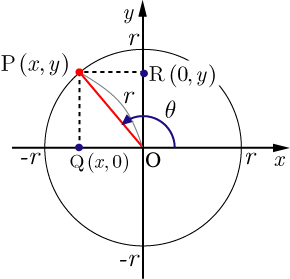



三角関数の相互関係




高校数学 三角方程式 不等式 三角関数の相互関係による関数の統一 受験の月



1




三角関数の公式の一覧 Wikipedia
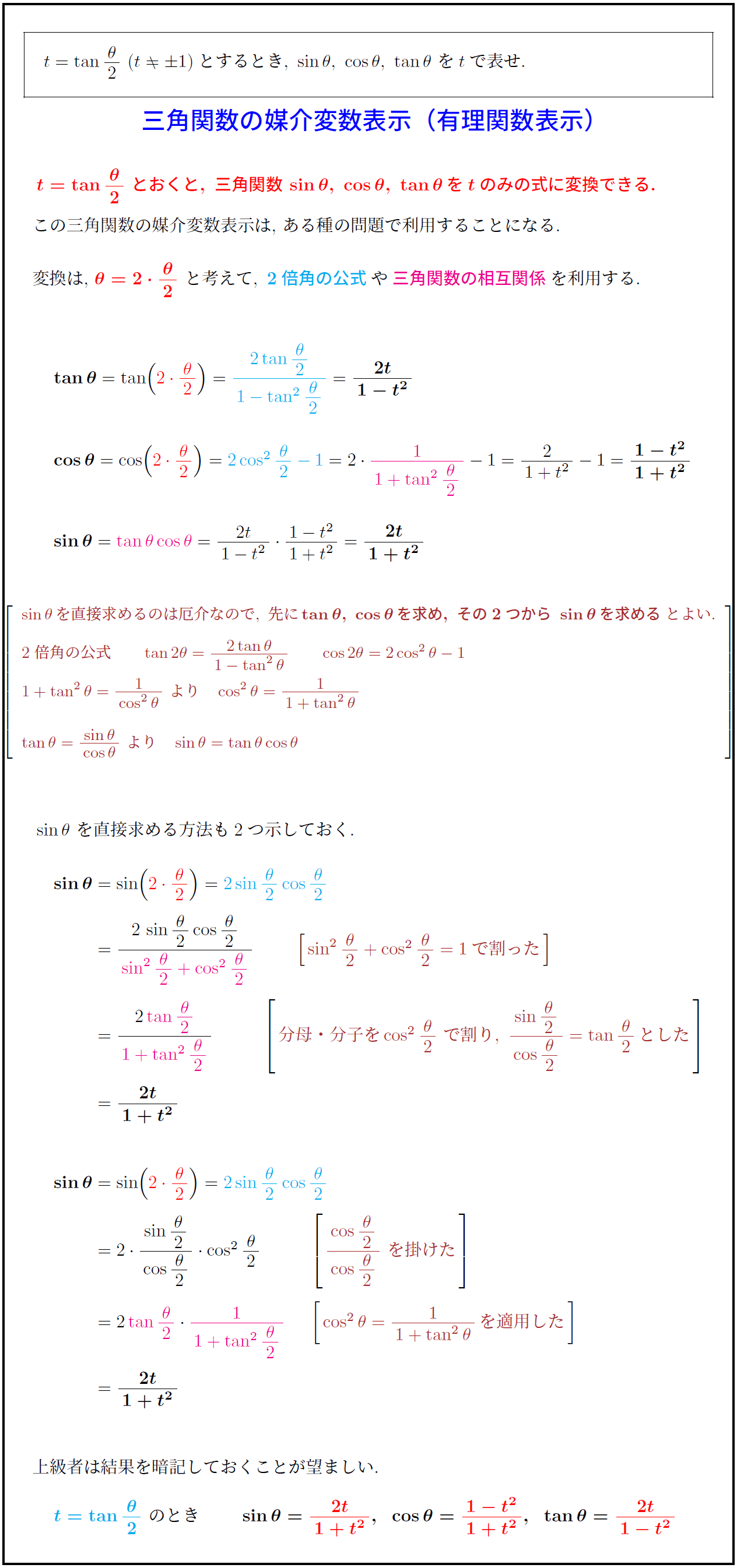



高校数学 三角関数の媒介変数表示 有理関数表示 T Tan 8 2 受験の月




高2 数2 三角関数の性質 公式まとめ 高校生 数学のノート Clear




三角関数の知識 やさしい電気回路




ม 5 โน ตของ 数2 三角関数の性質 公式まとめ ช น Senior Clear




高校数学 三角関数の相互関係を用いる証明 映像授業のtry It トライイット




高校数学 数 77 三角比 公式編 Youtube




高校数学 三角方程式 不等式 三角関数の合成 受験の月




三角関数とは コトバンク




高2 数学ii B 三角比 三角関数公式まとめ 高校生 数学のノート Clear



48s96ub7b0z5f Net Sankakukansuu Seishitsu



三角関数の積分 京極一樹の数学塾



三角関数の合成とは 公式 証明 最大最小や範囲の問題 受験辞典
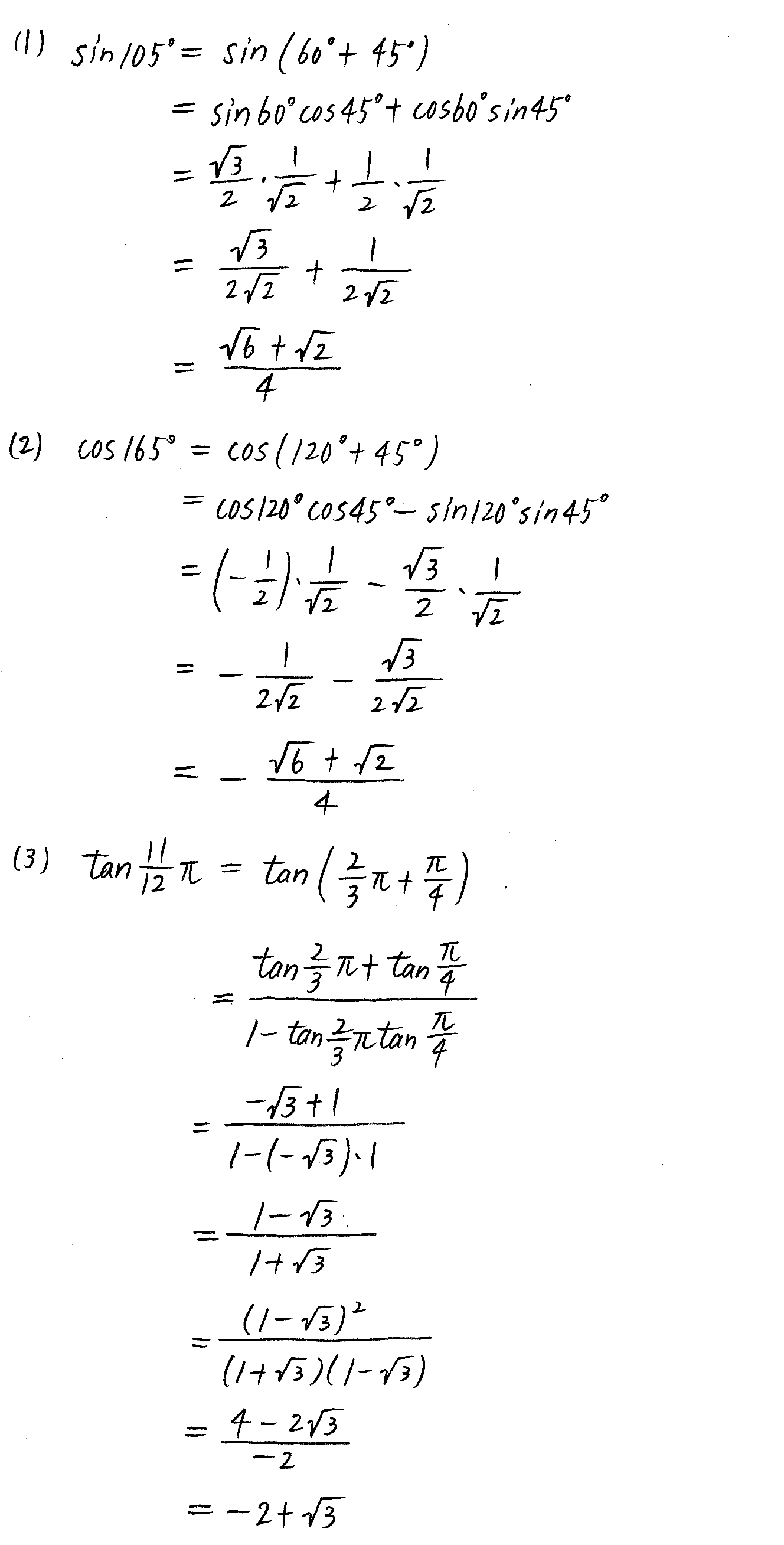



クリアー数学 数2 P61 27 三角関数の加法定理



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典



三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com



三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要




うさぎでもわかる解析 高校数学 数3 Part08 倍角の公式 和積の公式を用いた三角関数の積分 工業大学生ももやまのうさぎ塾
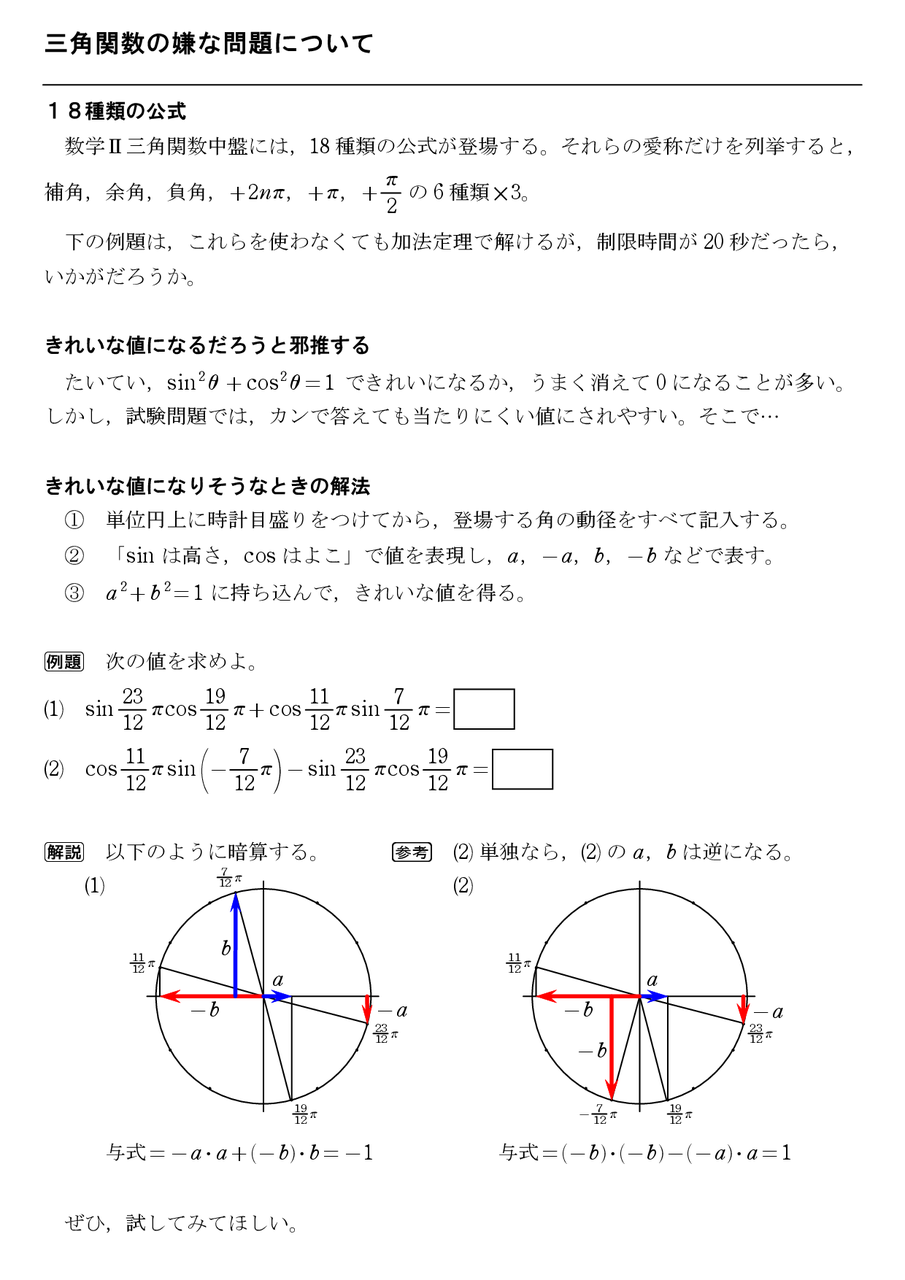



三角関数の嫌な問題について 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 三角関数 公式一覧 変換 倍角 半角 3倍角 合成関数 学校よりわかりやすいサイト




三角関数の合成 おいしい数学
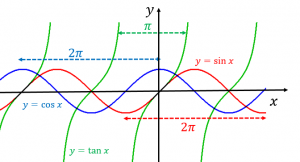



三角関数の周期の求め方と例題6問 具体例で学ぶ数学




逆三角関数 Wikipedia



3



数学2 三角関数 高校数学の難関 三角関数の重要ポイントがわかります




数 三角関数 Clear



0 件のコメント:
コメントを投稿