直角三角形の左端の角度が30度の時の比率は次のようになります。 1対2対√3(いったいにたいルートさん) (対辺a=1、斜辺b=2、底辺c=√3) 直角三角形の左端の角度が45度(直角二等辺三角形)の時の比率は次のようになります。面積の計算 ・ 正三角形の面積 ・ 三角形の面積 (底辺と高さ) ・ 三角形の面積 (2辺と間の角度) ・ 三角形の面積 (1辺と両端の角度) ・ 三角形の面積 (3辺の長さ) ・ 正方形の面積底辺と高さ 底辺は,三角形や平行四辺形などで,高さを測るための基準にとった辺のことをいいます。 高さは,三角形でいえば,頂点からその対辺 (底辺)へ垂直に引いた長さのことをいいます。 したがって,下のように,三角形のどの辺を底辺にとるかにより,高さもそれぞれ異なる位置に表されることになります。

二等辺三角形に関するある問題 底辺 高さそして面積 身勝手な主張
三角形 の 底辺
三角形 の 底辺-底辺と角度を入力し「高さ・斜辺・面積を計算」ボタンをクリックすると、入力された直角三角形の高さと斜辺と面積が表示されます。 底辺a: 角度θ: 度 ラジアン底辺aが1、斜辺cが2の直角三角形 高さ b: 角度 θ(度):60 ° 角度 θ(ラジアン): rad 面積 S:
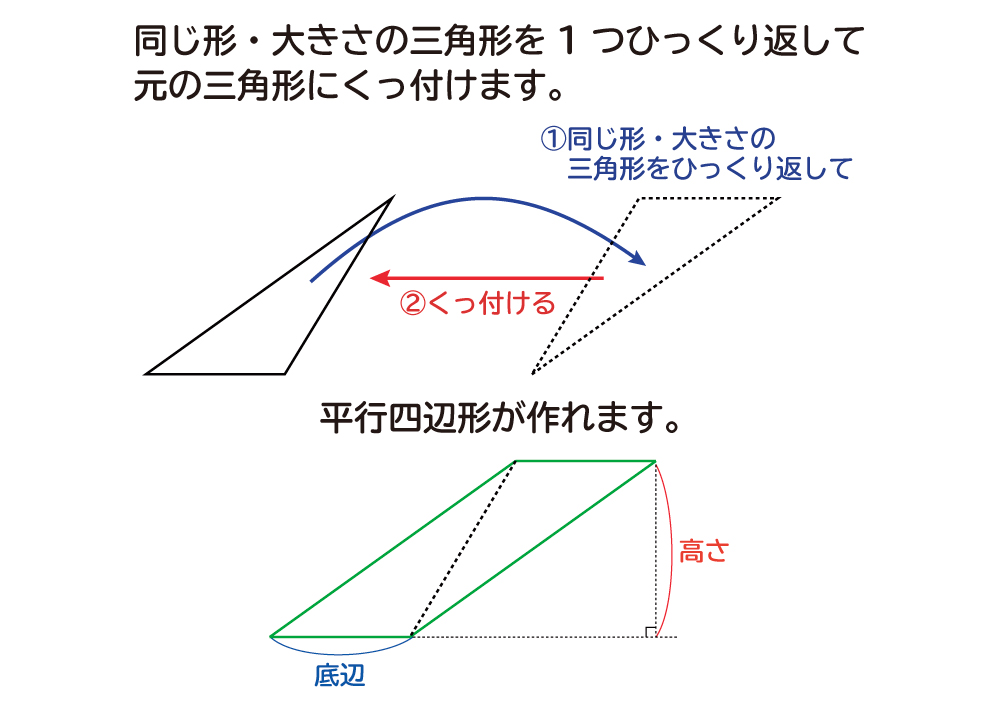



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
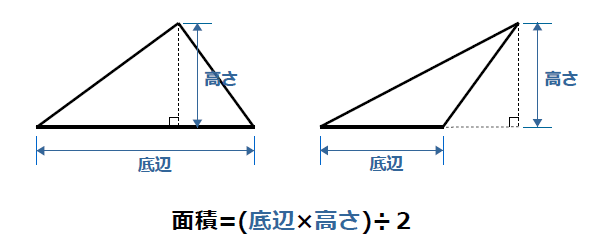
Right triangle (1) cosθ = a c , sinθ= b c , tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e ( 1) cos θ = a c , sin θ = b c , tan θ = b a ( 2) P y t h a g o r e a n t h e o r e m a 2 b底辺 (ていへん)は、 多角形 などの「底部」にある 辺 である。 ただし、 図形 に絶対的な 上下 はないので、紙面や画面上での向きとは無関係に、 計算 などに便利なように底辺を選ぶことができる。三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。
三角形の内心 ・ 外心 ・ 重心 三角形の3つの内角の2等分線は、1点で交わり、その点から3辺までの距離は等しい。 この1点で交わった点 I を三角形の内心という。 半径 IL の円が三角形の内接円である。・直角三角形(底辺と高さ) 直角三角形の底辺と高さから、斜辺と角度と面積を計算します。 ・ 直角三角形(底辺と斜辺) 直角三角形の底辺と斜辺から、高さと角度と面積を計算します。The latest tweets from @triangle08
三角形 底辺の求め方 (小学生) 三角形の高さと面積から底辺を求める方法がわかりません。 面積=底辺×高さ÷2 高さ=面積×2÷底辺 上記のように簡単に求められる公式が知りたいです。 よろしくおねがいします。 ちなみに問題は高さ19cm 面積171cm2の三角形 直角三角形の底辺と高さから傾斜角と斜辺を計算します。 底辺と高さから角度と斜辺を計算 高精度計算サイト ゲストさん まとめ:二等辺三角形の底辺は二等分線からはじまる。 二等辺三角形の底辺の計算は簡単。 頂角の二等分線を底辺にひく 底辺の半分の長さを求める そいつを2倍する っていう3ステップでいいんだ。 どんどん問題をといてみよう! そんじゃねー Ken



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典




円の特徴 同じ弦をもつ三角形 数学a By Okボーイ マナペディア
下図の二等辺三角形の頂角を求めてください。 簡単ですね。底角が30°と分かっています。よって 頂角=180-2×30=1° です。二等辺三角形の詳細は下記が参考になります。 二等辺三角形の底辺は?三角形は(角度を除いた場合)3つの寸法が必要です。 底辺・高さ・底辺以外の1辺の長さ(隣接の三角形の底辺になっている)。 これがわかっているところから三角形を書きます。 複線、円弧(コンパス代わり)、接線(これを使うのがミソ?精選版 日本国語大辞典 底辺の用語解説 〘名〙① 三角形の頂点に対する辺。三角形で高さを測るために基準にとった辺。二等辺三角形の等辺でない辺。〔数学ニ用ヰル辞ノ英和対訳字書(18)〕② 物事の底の部分。特に、社会の下層部。※日本の思想(1961)〈丸山真男〉i「近代国家の政



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係



3
二等辺三角形で、長さの等しい 2 つの辺を 等辺 といい、残りの 1 つの辺を二等辺三角形の 底辺 と呼ぶ。 2 つの等辺のなす角を 頂角 といい、残りの 2 つの内角を 底角 という。直角三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と角度 斜辺と高さ 斜辺と角度 高さと角度 面積と底辺 面積と高さ 面積と斜辺 面積と角度底辺比分割の定理、 高さ比分割の定理、 直角三角形の相似 今日の受験クラスは、 速さと比、 図形と相似比、 だった。 距離÷時間の図解は、直角三角形であらわす。 速さ×時間は、面積であらわす。 となると、割り算は、直角三角形で、 掛け算は、面積で、それぞれ表現することになる。
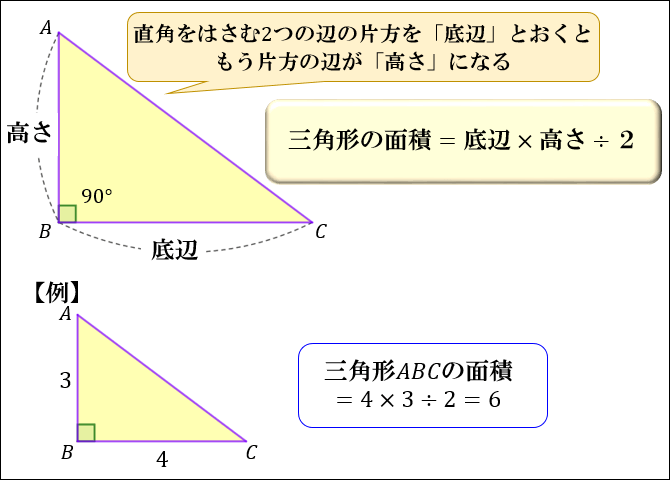



直角三角形の辺の長さ 合同条件 面積について アタリマエ




直角三角形の底辺と高さで角度を求める 電卓で墨だし計算 Teacup ブログ Autopage
中学校2年平行四辺形9/10時間・三角形と四角形17/19時間(東京書籍:新しい数学2 p141) 思考の開始 ・三角形の面積は,(底辺)×(高さ)÷2で求められ, どの三角形も底辺BCが等しく高さも等しいから。 ・底辺と高さが等しいから。長い辺(斜辺)を求める方法 直角三角形の直角をはさむ2つの辺の長さを a 、 b として、長い辺の長さを c とします。 このとき、 a × a b × b = c × c が成立します。 これを三平方の定理、またはピタゴラスの定理と言います。 例題1: 図のような直角三角形の長い辺の長さを求めよ。 長い辺の長さを c とすると、 なぜ、どんな形をした三角形でも、その面積は 「三角形の面積 底辺 高さ 」 「 三 角 形 の 面 積 = 底 辺 × 高 さ ÷ 2 」 で求まるのでしょうか。 形がちがう2種類の「底辺 5 c m 高さ 2 c m の三角形」を通じてみていきましょう。 ※1マス 1 c m 初めに、同じ形
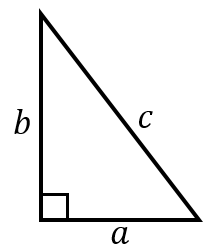



直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
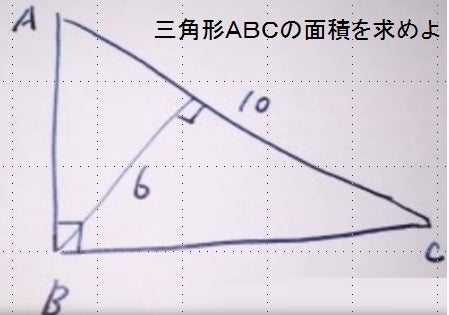
三角形であれば頂点が3つあれば良いので、 このように球面上の三角形(球面三角形)を作る事が出来ます。 ② 斜辺10cm、高さ6cmの「球面直角三角形」 球面三角形のある頂点の角度は、その頂点を通る2つの断面円(平面)が成す角度です。O (0, 0) とすると、直角三角形 A O C の面積は (t a) h 2 、直角三角形 A O B の面積は t h 2 ですから、 A B C の面積は (t a) h 2 − t h 2 = a h 2 となります。 以上により、底辺が a 、高さが h である任意の三角形の面積は a h 2 となることが示せました。 三角形の面積はなぜ底辺×高さ÷2で求められるの? 三角形は大きく分けて3種類あります。 直角三角形 1 3角形の角のうち1つが90°である三角形のことをいいます。 、鋭角三角形 2 三角形の3つの角、全てが90°より小さい三角形のことをいいます。 、鈍角三角形 3 三角形の角のうち1つの




平面図形をマスター 三角形の面積比 応用編その3



第1巻 命題8 二つの三角形があって 2辺がそれぞれ等しく また底辺が等しかったら それぞれ等しかった2辺に挟まれた角は互いに等しい 数学雑記 楽天ブログ
鈍角三角形abcの面積=直角三角形abdの面積ー直角三角形acdの面積とも言えます。 少しややこしかったですね。お疲れさまでした。 公式を使えば三角形の面積なんてすぐに計算できます。 三角形の面積=底辺×高さ÷2は、直角三角形と鋭角三角形は簡単に直角三角形の底辺と傾斜角から斜辺と高さを計算します。 底辺 a 角度 θ (525度は 525、5度12分6秒は 5'12'6 と入力) 6桁 10桁 14桁 18桁 22桁 26桁 30桁 34桁 38桁 42桁 46桁 50桁 斜辺 c
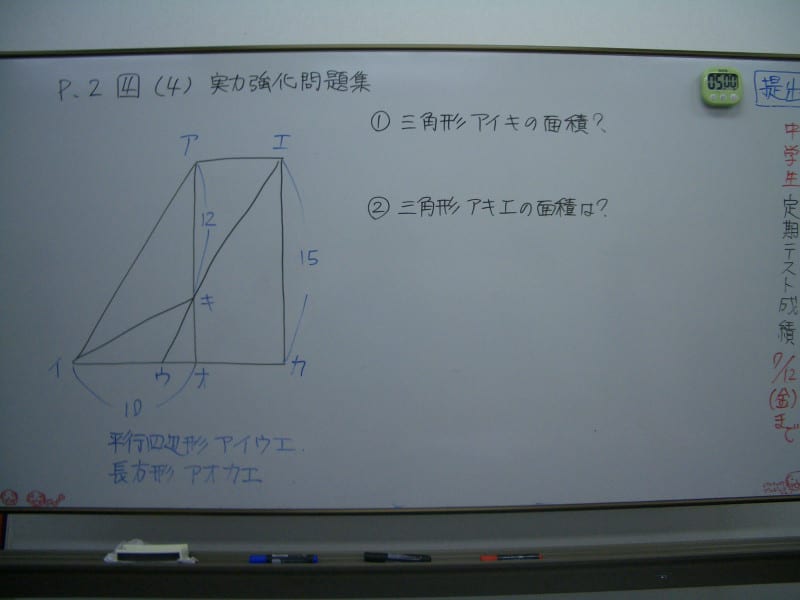



小6算数 三角形の底辺と高さが同じなら 面積は同じ ブログ アビット




面積の求め方 計算公式一覧



超有名it会社入社試験でのひっかけ問題 杉浦技術士事務所のブログ




二等辺三角形に関するある問題 底辺 高さそして面積 身勝手な主張
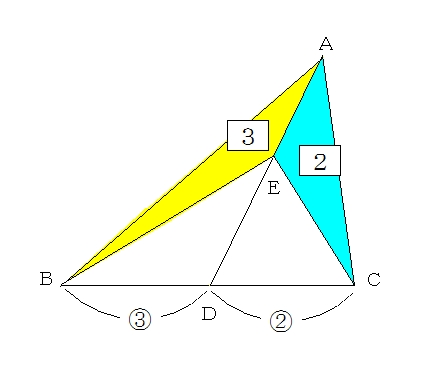



辺の比と面積比




底辺が共通な2つの三角形の角度について ある視覚生理系のテキストの 数学 教えて Goo
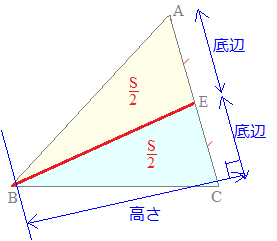



三角形の面積の二等分線
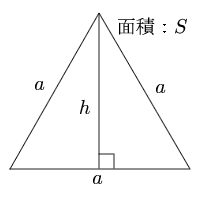



正三角形 辺から高さと面積 三角形の計算 計算サイト




二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web
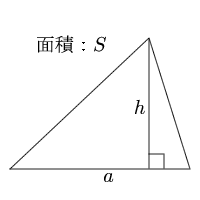



三角形の底辺と高さ 面積の計算 計算サイト
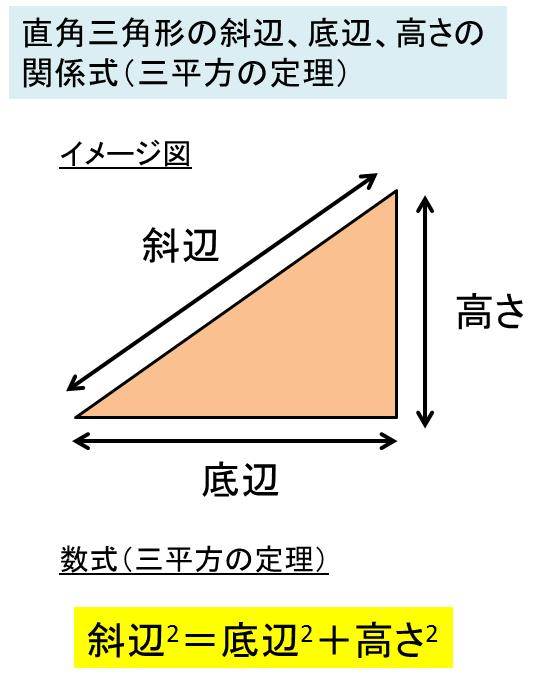



Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方
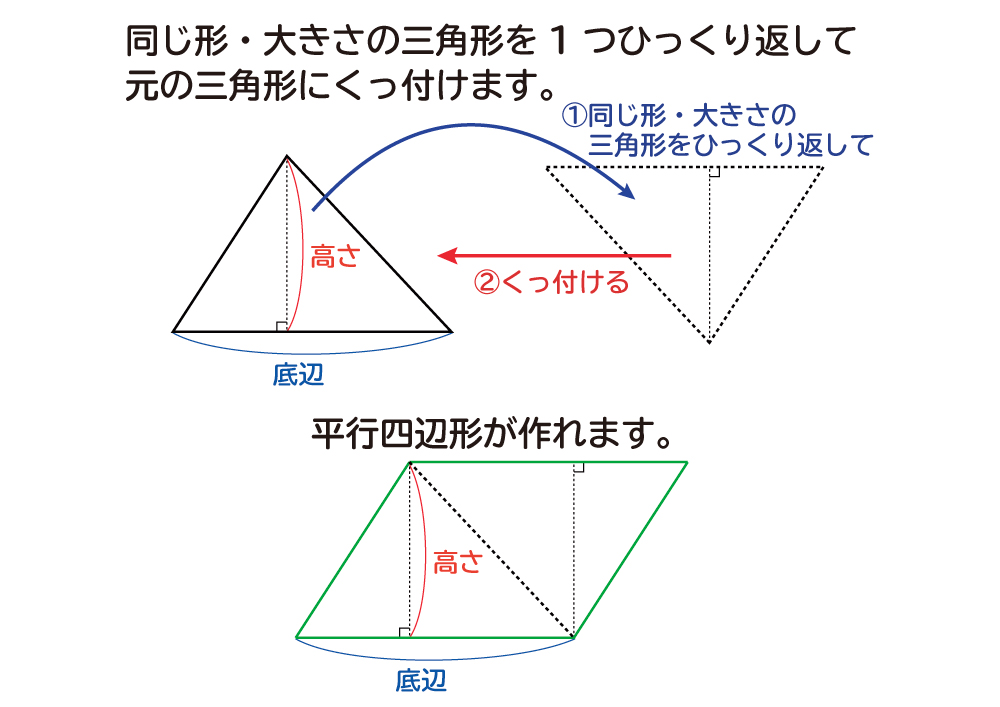



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル




Scm2 Descubre Como Resolverlo En Qanda




三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校




平面図形をマスター 三角形の面積比 応用編その3




頂角の二等分線は底辺を二等分する Youtube




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




二等辺三角形の頂点から下ろした線が底辺の中点を通る時 それは頂角の二等分線であり 底 Clear



三角形の辺の比による三角関数の定義
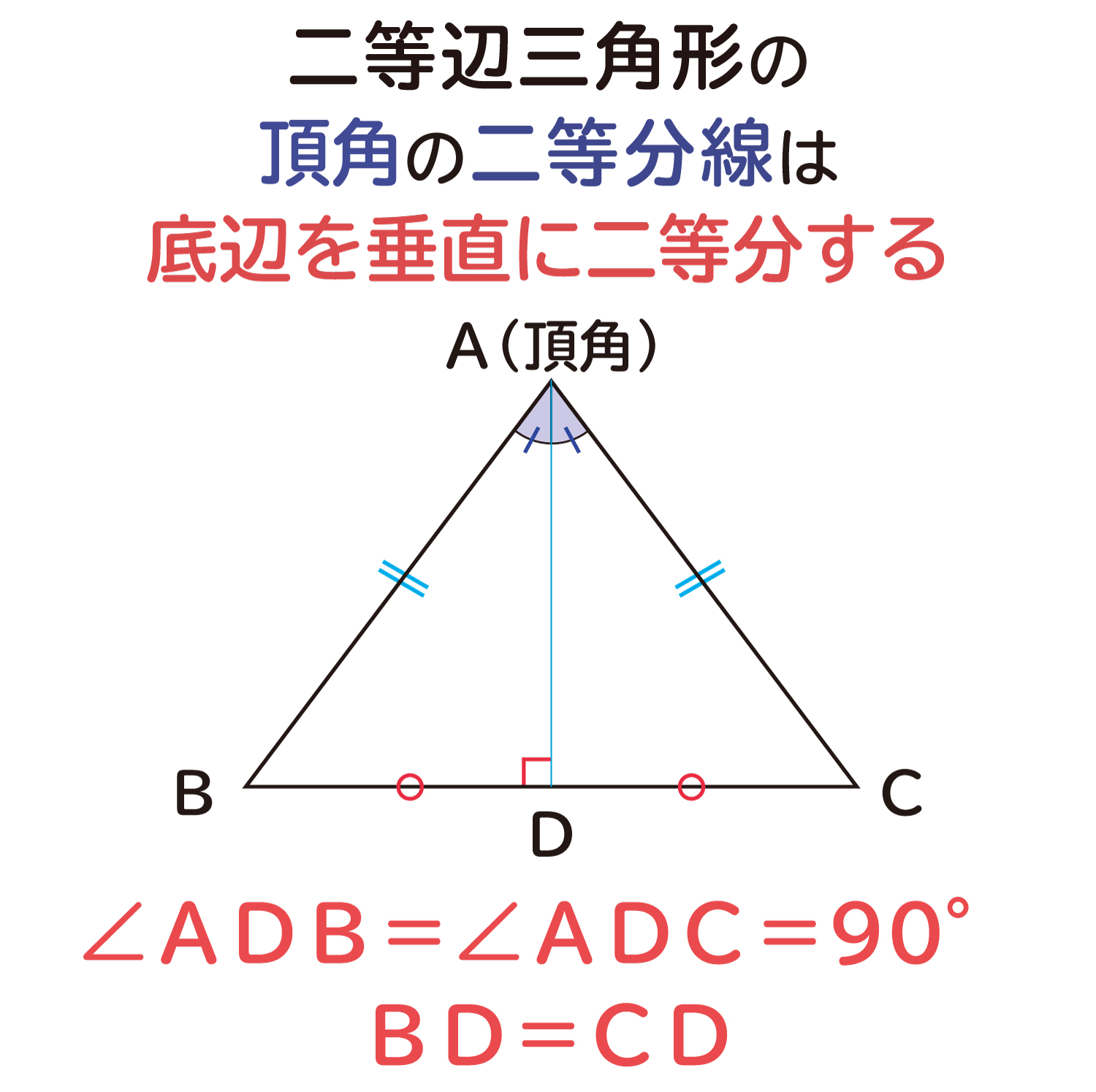



二等辺三角形の頂角の二等分線は 底辺を垂直に二等分する ことの説明 おかわりドリル
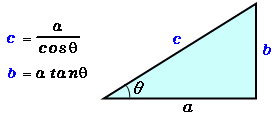



角度と底辺から斜辺と高さを計算 高精度計算サイト




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
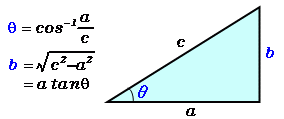



底辺と斜辺から角度と高さを計算 高精度計算サイト



Math Battle 06 三角形の底辺の中点
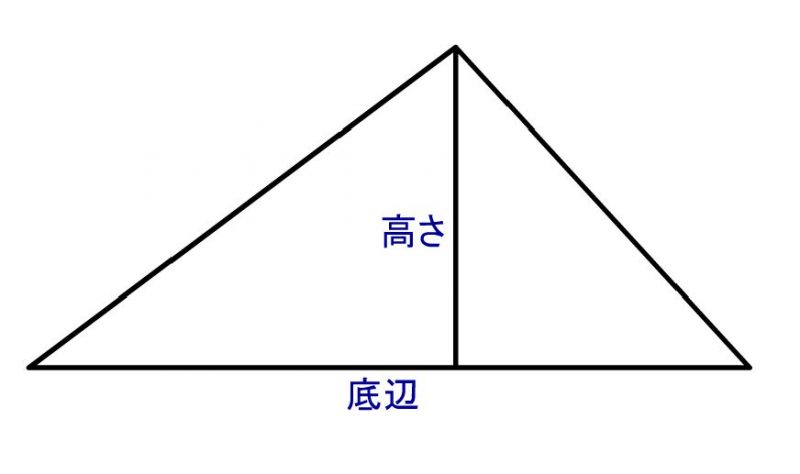



三角形の面積 底辺 高さ 2 をシミュレーションで復習しよう 数学入門




直角三角形の角から垂線を引いたときの底辺の比の問題 の裏ワザ 大阪のプロ家庭教師が できない を できる に変える
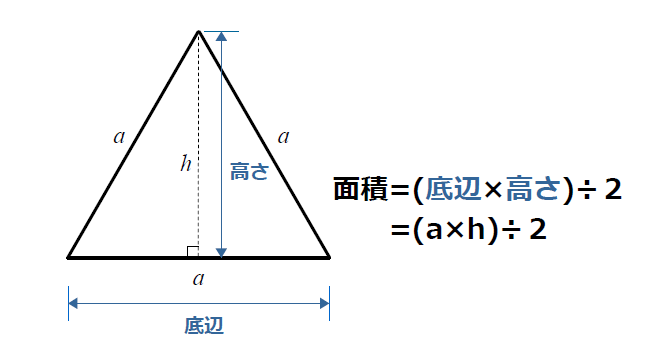



正三角形の面積計算 ゆるゆるプログラミング




底辺と高さから角度と斜辺を計算 高精度計算サイト




Pe10xcm 30 Cm23 Descubre Como Resolverlo En Qanda




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




平面図形をマスター 三角形の面積比 応用編その3




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




底辺 Wikipedia



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



三角形の面積計算 ゆるゆるプログラミング
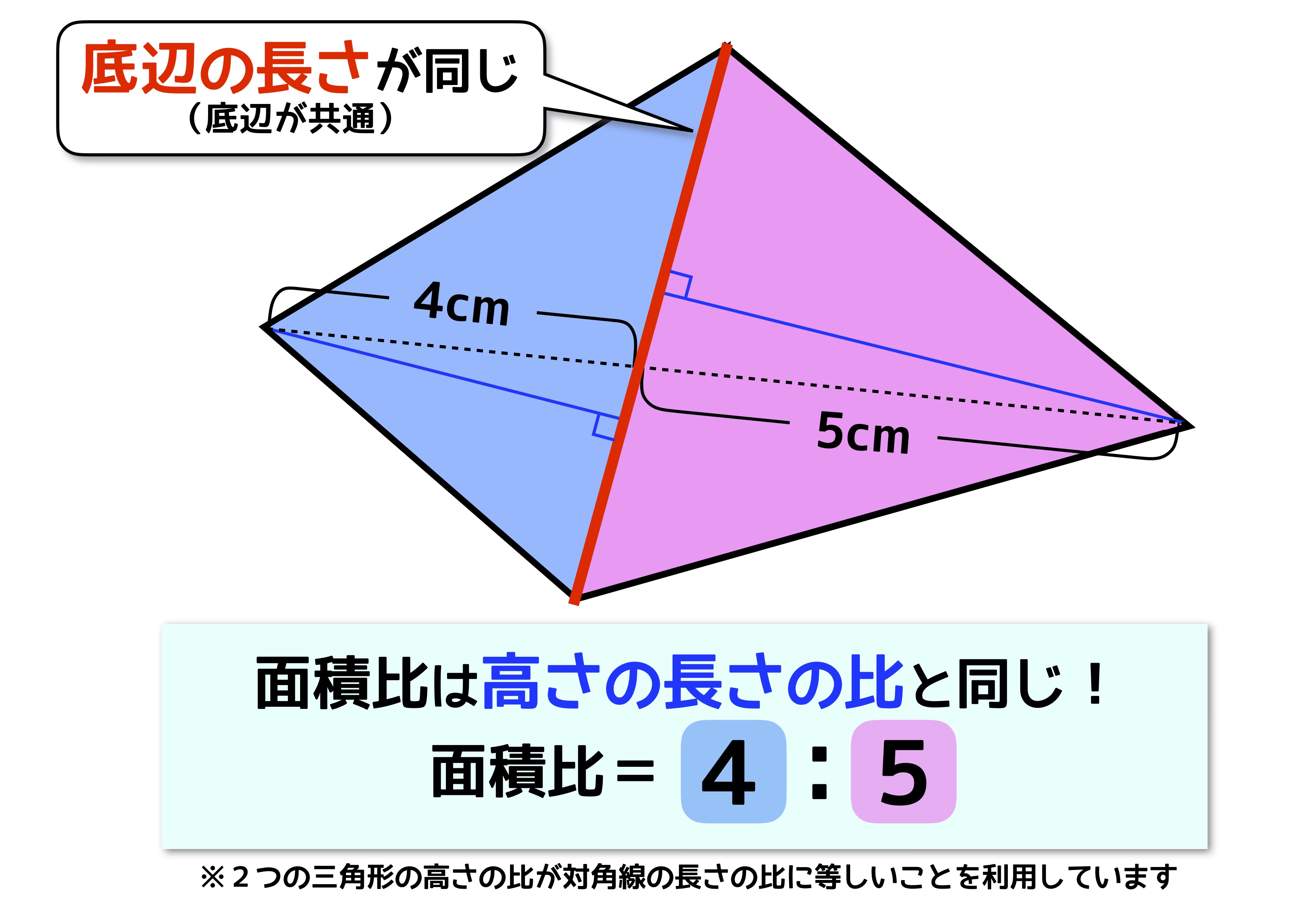



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
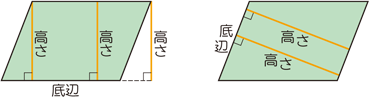



底辺と高さ 算数用語集
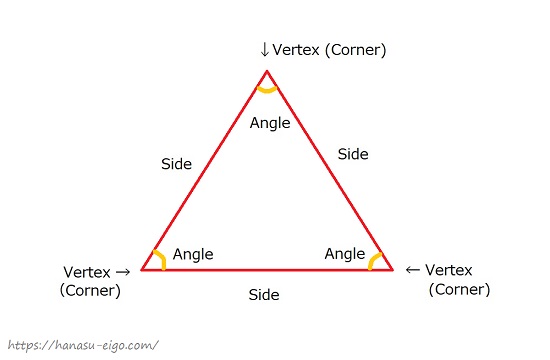



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語
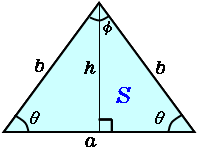



二等辺三角形 高精度計算サイト
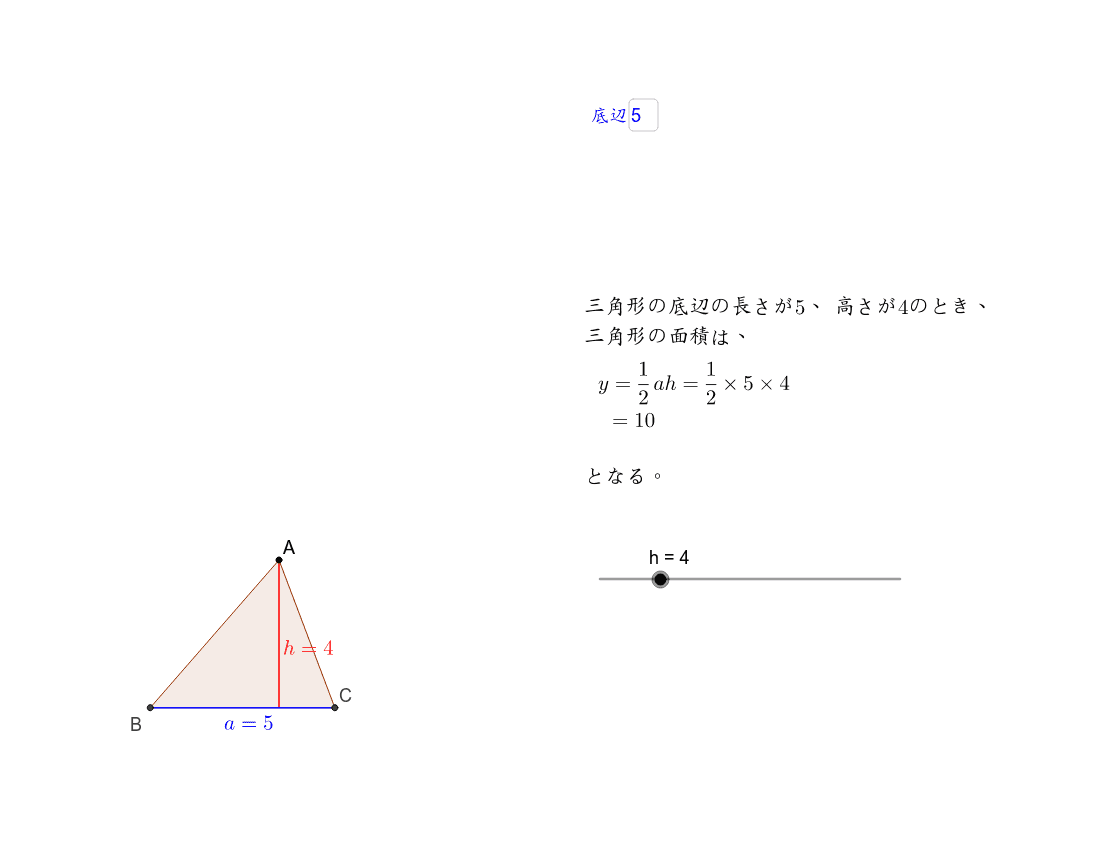



三角形の面積を表現する文字式 Geogebra
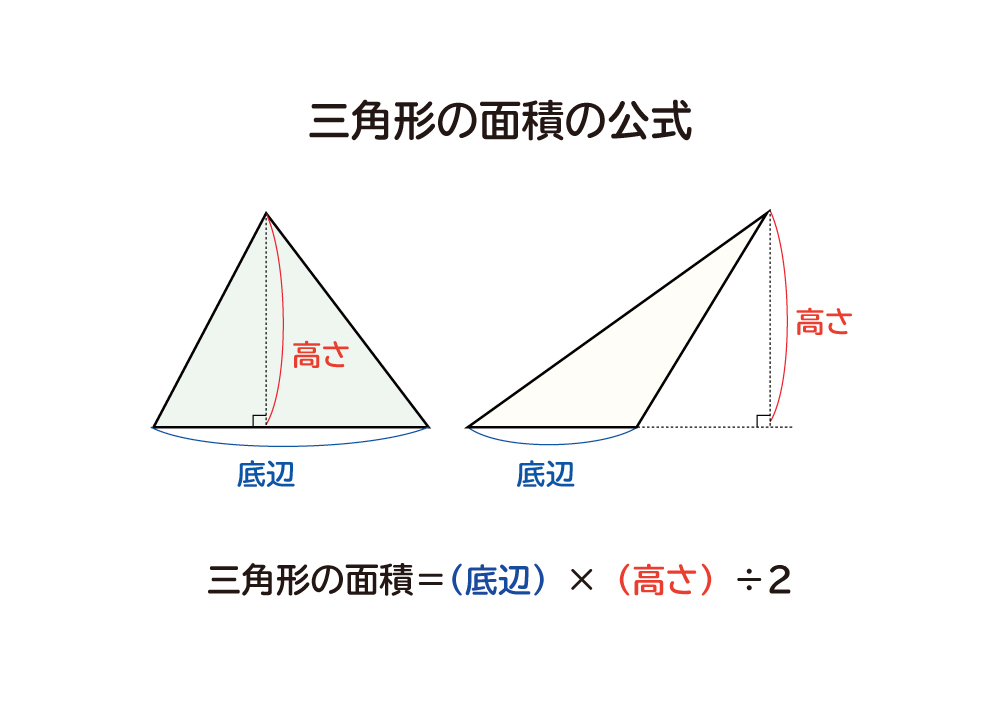



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル




三角形の頂角の2等分線が底辺をわけるときの比 身勝手な主張




電験三種の数学 三角比 対辺と底辺の見分け方 電験3種ネット



1
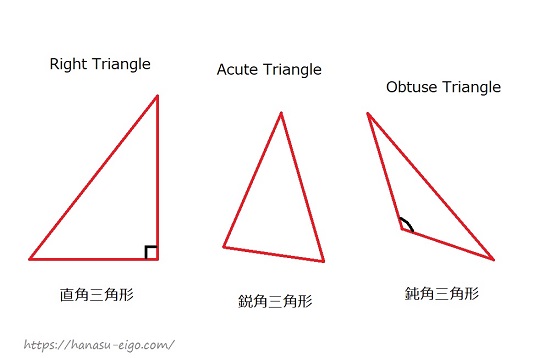



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



図形の扉 面積のひみつ




電験三種の数学 三角比 対辺と底辺の見分け方 電験3種ネット



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める
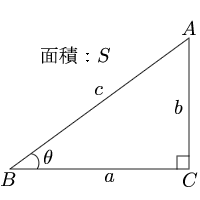



直角三角形 底辺と斜辺 三角形の計算 計算サイト




5年算数面積2 教え方のポイント
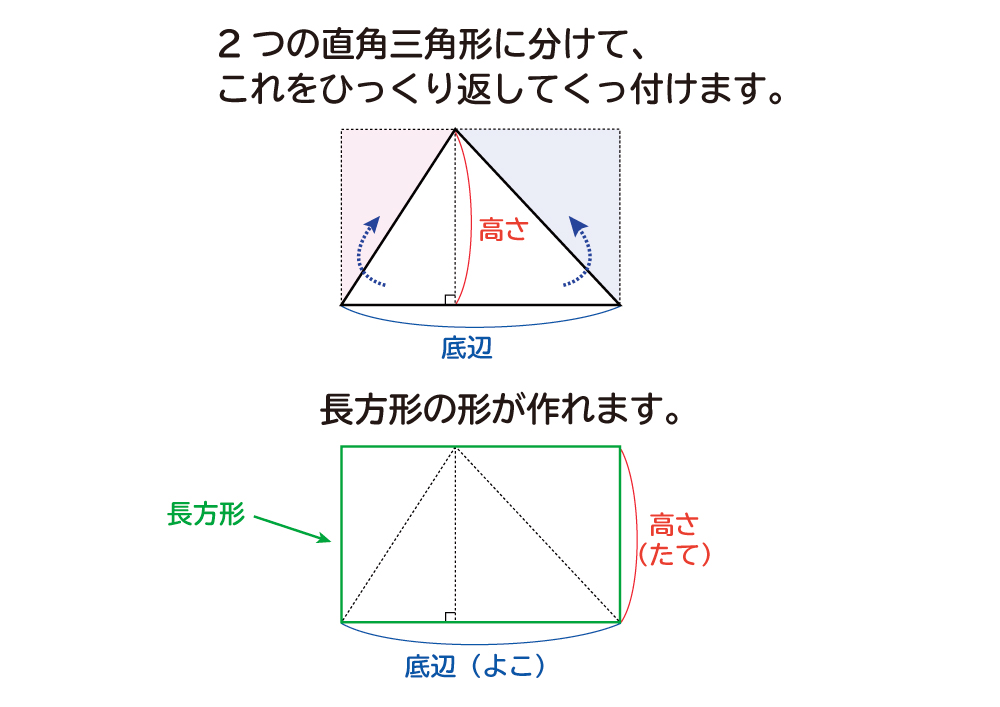



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル




三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語




三角形の面積の求め方 絶対に覚えておきたい超大切な公式 中学や高校の数学の計算問題
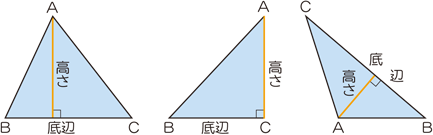



底辺と高さ 算数用語集
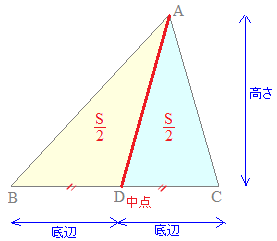



三角形の面積の二等分線




マスラボ 小学5年生 三角形の面積 高さや底辺を求める Youtube




なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
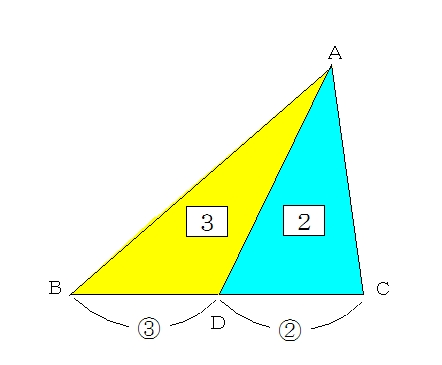



辺の比と面積比




数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




大至急です 相似 面積比の問題です Clear
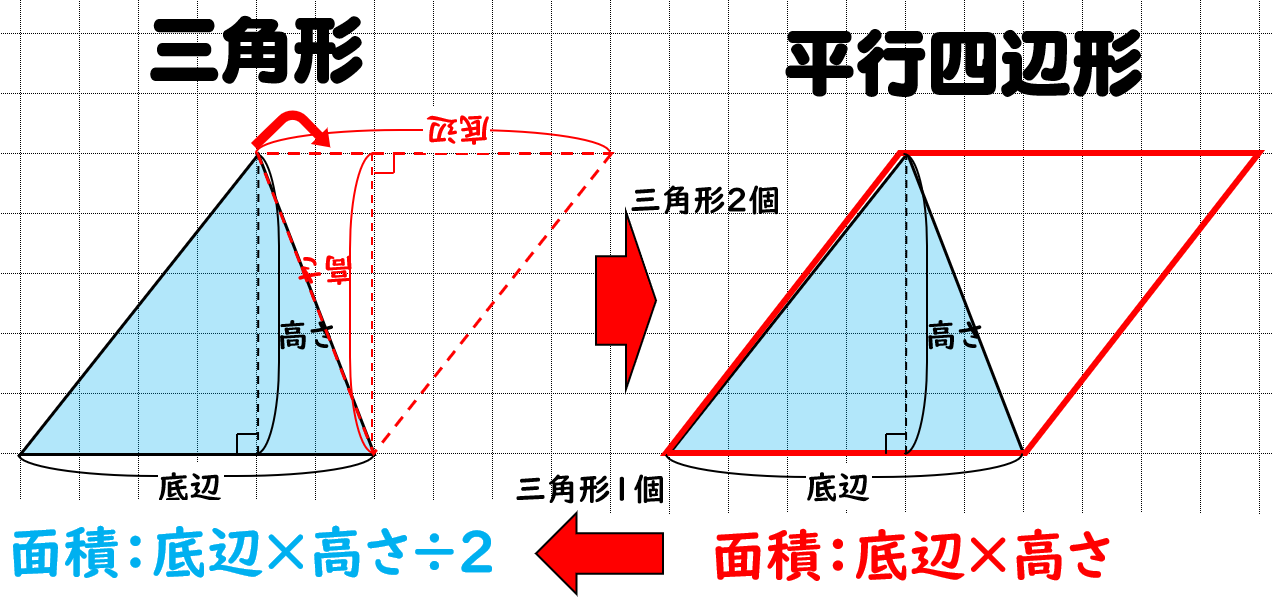



三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



直角三角形の底辺の長さは 1分でわかる計算 斜辺 高さ 角度との関係
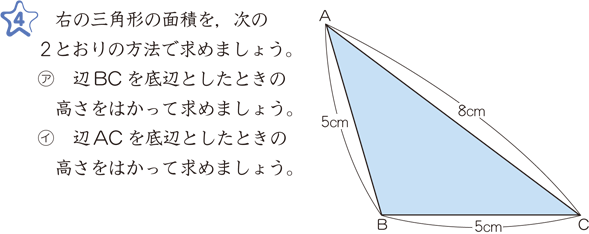



底辺と高さ 算数用語集




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



Q Tbn And9gct71t318twmynw63dxmqoj5dsomuiz6o0rnzjk6hursgayaq9 L Usqp Cau




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
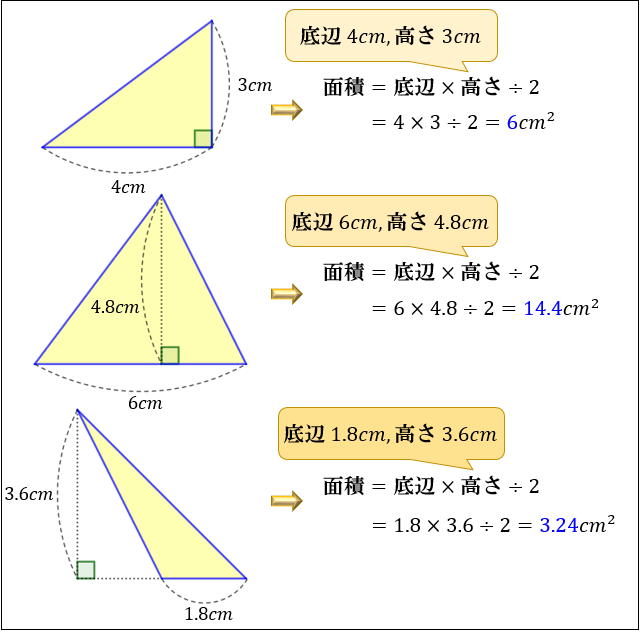



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ




Mondai74




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算
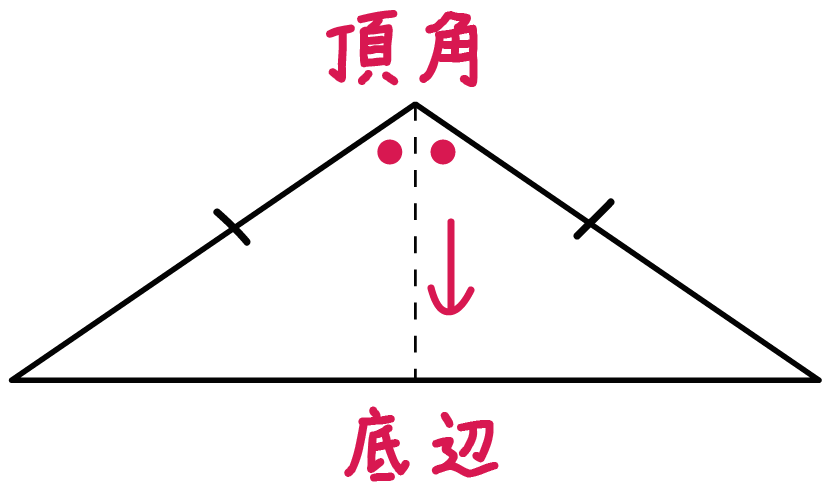



二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




二等辺三角形 ゆるゆるプログラミング
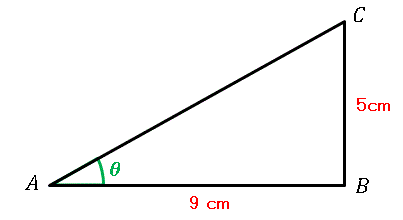



Excel で直角三角形の斜辺と底辺に挟まれた角度を求めます



1
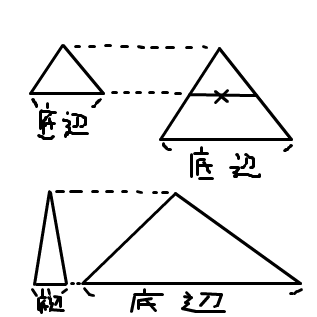



底辺とは テイヘンとは 単語記事 ニコニコ大百科



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係
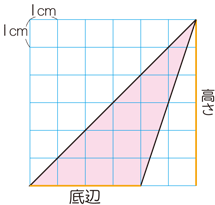



底辺と高さ 算数用語集




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ
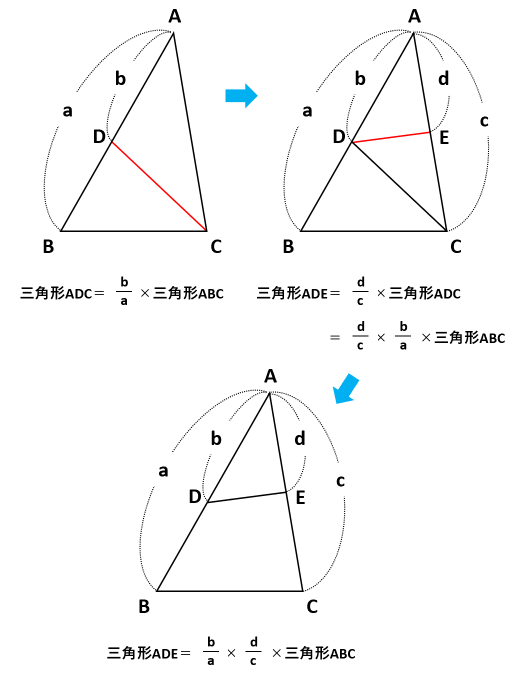



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




これまでで最高の三角形 の 底辺 子供のための最高のぬりえ




三角形の高さの求め方 底辺の位置によって 高さは変わる 中学や高校の数学の計算問題




写真のように真ん中の線分と三角形の底辺が平行で 底辺の中点と三角形の1番上の頂点を通 Clear
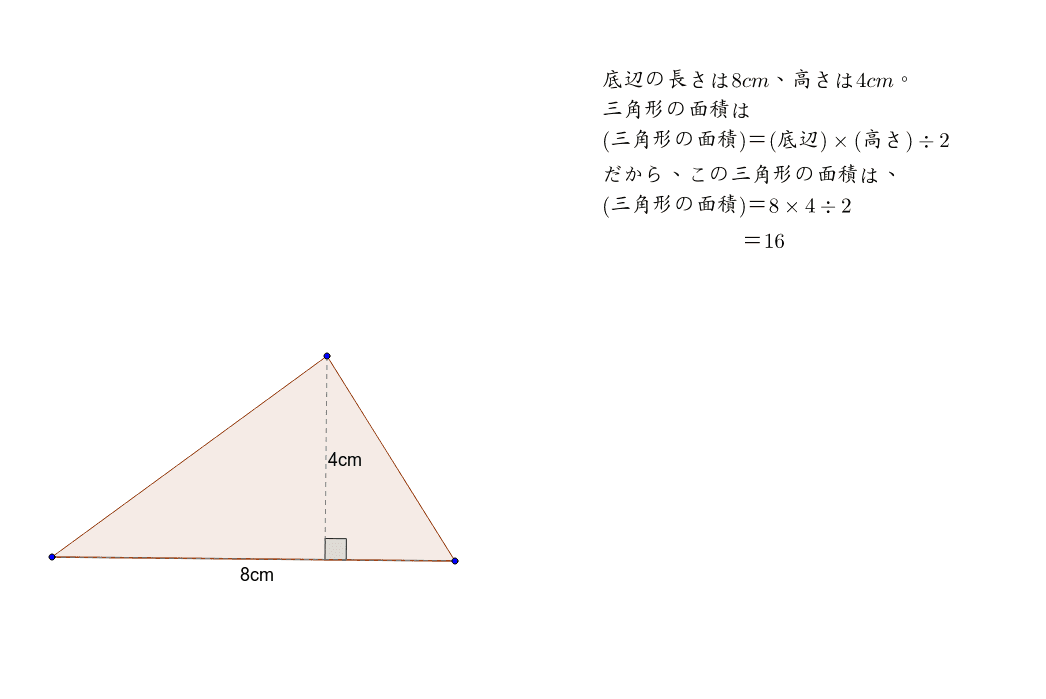



三角形の面積 Geogebra
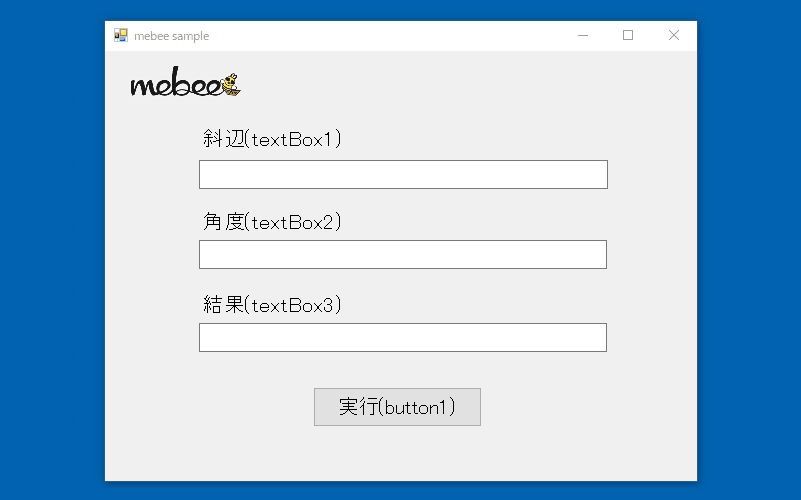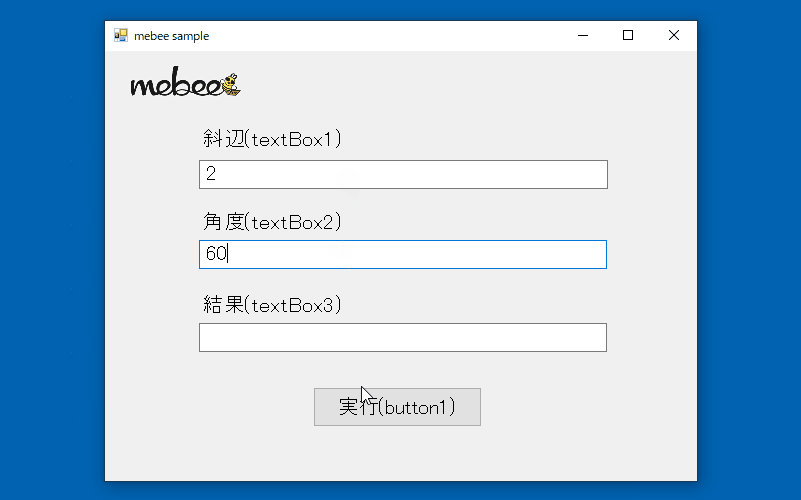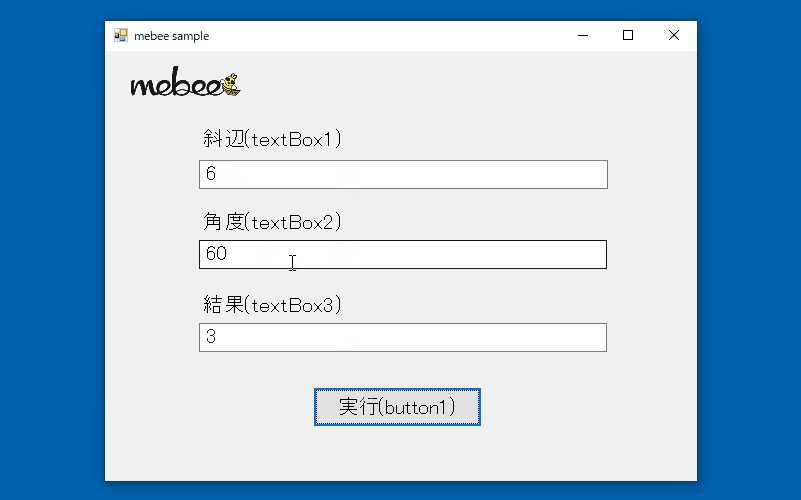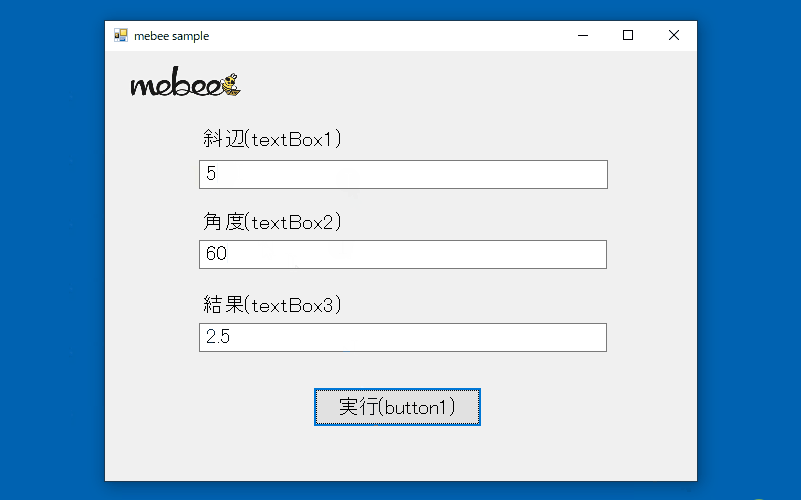



C Cosメソッドを使用して直角三角形の底辺の長さを求める Mebee




二等辺三角形の面積を求める算数の公式は



二等辺三角形の公式 面積 高さ 角度 斜辺と周囲の長さ 数学 エクセルマニア



第1巻 命題7 底辺が同じで 同じ底辺の端点から延びている線分が同じ二つの三角形があるとき 底辺と同じ側に頂点を配したとき その頂点は異なる位置に配せない 数学雑記 楽天ブログ
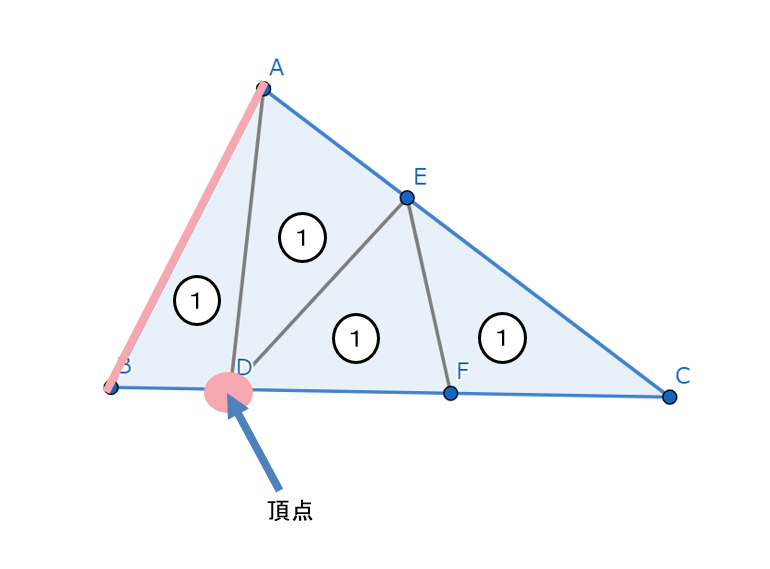



高さの等しい三角形の見つけ方 底辺探し 中学受験プロ講師ブログ




三角形の面積の公式はどうして底辺 高さ 2なのか Irohabook



0 件のコメント:
コメントを投稿